3 Data Preparation in Practice: From Raw Data to Insight
An approximate answer to the right question is worth a great deal more than a precise answer to the wrong one.
You have just been handed a spreadsheet with hundreds of columns and thousands of rows—full of missing entries, inconsistent labels, strange codes like -999, and values that defy logic. How do you begin to turn this chaos into insight?
In this chapter, we explore one of the most underestimated yet indispensable stages in the Data Science Workflow: data preparation. No matter how sophisticated your algorithm, the quality of your data ultimately determines the credibility of your results. It is often said that data scientists spend up to 80% of their time preparing data—and with good reason.
In real-world settings, data rarely arrives in a clean, analysis-ready format. It often contains missing values, outliers, and inconsistent entries. By contrast, datasets on platforms such as Kaggle are typically curated and neatly labeled, often with a clear target variable and well-posed analytical question. These are excellent for learning, but they can give a misleading impression of what real data science work involves. In practice, data is collected for operational rather than analytical purposes, and significant effort is required to make it suitable for decision-making.
To illustrate data preparation techniques, we begin with the diamonds dataset from the ggplot2 package—a structured and relatively clean dataset ideal for learning foundational skills. Later in the chapter, we turn to the adult income dataset, where the same techniques are applied in a more realistic and challenging context.
Although this chapter focuses on preparing and cleaning data, several steps—such as detecting outliers and handling missing values—overlap with Exploratory Data Analysis (Chapter 4) and Setting Up Data for Modeling (Chapter 6). These stages are often revisited in practice, reflecting the iterative nature of the Data Science Workflow.
With a clear understanding of the problem and its relationship to the available data, we now move to the practical task of preparing the dataset for analysis. This step builds the foundation for meaningful insights and reliable machine learning models, transforming raw information into structured knowledge.
What This Chapter Covers
This chapter introduces the essential techniques for transforming raw data into a format suitable for analysis and modeling. You will learn how to:
Identify and manage outliers using visualization and filtering to reduce distortion.
Detect and impute missing values to maintain data quality and completeness.
We begin by clarifying the analytical goals of the diamonds dataset and framing the task of price estimation as a data science problem. The chapter concludes with a hands-on case study using the adult income dataset, where you will apply the complete data preparation pipeline in a more complex, real-world context. Together, these skills form a crucial part of the Data Science Workflow and prepare you to build models with clean, structured, and meaningful data.
3.1 Data Preparation in Action: The diamonds Dataset
How can we quantify the value of a diamond? What determines why two stones that appear nearly identical fetch vastly different prices? In this section, we bring the concepts of data preparation to life using the diamonds dataset, a rich, structured collection of gem attributes from the ggplot2 package. It serves as our testing ground for exploring how to clean, transform, and organize data in ways that reveal meaningful insights.
Our central goal is to understand how features such as carat, cut, color, and clarity contribute to price variation. But before we begin processing the data, we must first frame the business problem and identify the analytical questions it raises. Data preparation is not merely technical; it is purposeful.
We focus on three guiding questions: which features have the strongest influence on diamond price; whether consistent pricing patterns emerge based on attributes like carat weight or cut quality; and whether the dataset contains anomalies, such as outliers or inconsistent entries, that must be addressed before modeling.
From a business perspective, answering these questions supports smarter pricing and inventory strategies for jewelers and online retailers. From a data science perspective, it ensures that our preprocessing choices, such as filtering outliers or encoding variables, are aligned with the real-world task at hand. This alignment between domain understanding and technical preparation is what makes data preparation both effective and impactful.
Later in the book, we will return to this dataset in Chapter 10, where we use the features prepared here to build a predictive regression model, completing the journey from raw data to actionable insight.
Overview of the diamonds Dataset
With a clear understanding of the problem and the analytical goals, we are ready to begin working directly with the data. The first step in data preparation is to load the dataset and explore its structure to identify what needs to be cleaned, transformed, or encoded.
We use the diamonds dataset from the ggplot2 package, a structured collection of gem characteristics such as carat weight, cut, color, clarity, and price. This dataset serves as a clean but realistic foundation for practicing core data preparation techniques.
The dataset includes over 50,000 rows, with each observation representing a unique diamond. It provides 10 variables describing physical attributes and quality ratings. To follow along in R, make sure the ggplot2 package is installed. If it is not yet installed, install it with install.packages("ggplot2"). Then load the package and access the dataset:
To get a sense of the dataset’s structure, use the str() function:
str(diamonds)
tibble [53,940 × 10] (S3: tbl_df/tbl/data.frame)
$ carat : num [1:53940] 0.23 0.21 0.23 0.29 0.31 0.24 0.24 0.26 0.22 0.23 ...
$ cut : Ord.factor w/ 5 levels "Fair"<"Good"<..: 5 4 2 4 2 3 3 3 1 3 ...
$ color : Ord.factor w/ 7 levels "D"<"E"<"F"<"G"<..: 2 2 2 6 7 7 6 5 2 5 ...
$ clarity: Ord.factor w/ 8 levels "I1"<"SI2"<"SI1"<..: 2 3 5 4 2 6 7 3 4 5 ...
$ depth : num [1:53940] 61.5 59.8 56.9 62.4 63.3 62.8 62.3 61.9 65.1 59.4 ...
$ table : num [1:53940] 55 61 65 58 58 57 57 55 61 61 ...
$ price : int [1:53940] 326 326 327 334 335 336 336 337 337 338 ...
$ x : num [1:53940] 3.95 3.89 4.05 4.2 4.34 3.94 3.95 4.07 3.87 4 ...
$ y : num [1:53940] 3.98 3.84 4.07 4.23 4.35 3.96 3.98 4.11 3.78 4.05 ...
$ z : num [1:53940] 2.43 2.31 2.31 2.63 2.75 2.48 2.47 2.53 2.49 2.39 ...This command reveals the number of observations and variables, along with data types and sample values. The dataset includes numerical features such as carat (weight), price, and physical dimensions (x, y, z), as well as categorical attributes like cut (quality of cut), color (ranging from D to J), and clarity (from I1 to IF). These features are central to the modeling task we will revisit in Chapter 10.
Here is a summary of the key variables:
-
carat: weight of the diamond (ranging from 0.2 to 5.01), -
cut: quality of the cut (Fair, Good, Very Good, Premium, Ideal), -
color: color grade, from D (most colorless) to J (least colorless), -
clarity: clarity grade, from I1 (least clear) to IF (flawless), -
depth: total depth percentage calculated as2 * z / (x + y), -
table: width of the top facet relative to the widest point, -
x,y,z: physical dimensions in millimeters, -
price: price in US dollars (ranging from $326 to $18,823).
Before we can begin cleaning or transforming the data, we need to understand the types of features we are working with. Different types of variables require different preparation strategies. In the next section, we examine how the features in the diamonds dataset are structured and classified.
3.2 Identifying Feature Types
Before detecting outliers or encoding variables, it is crucial to understand what kinds of features we are working with. Whether a variable is numerical or categorical, and what subtype it belongs to, will shape how we clean, transform, and model the data. Feature types influence which visualizations make sense, which preprocessing steps are appropriate, and how machine learning algorithms interpret input values.
Figure 3.1 summarizes the main types of features commonly encountered in data science:
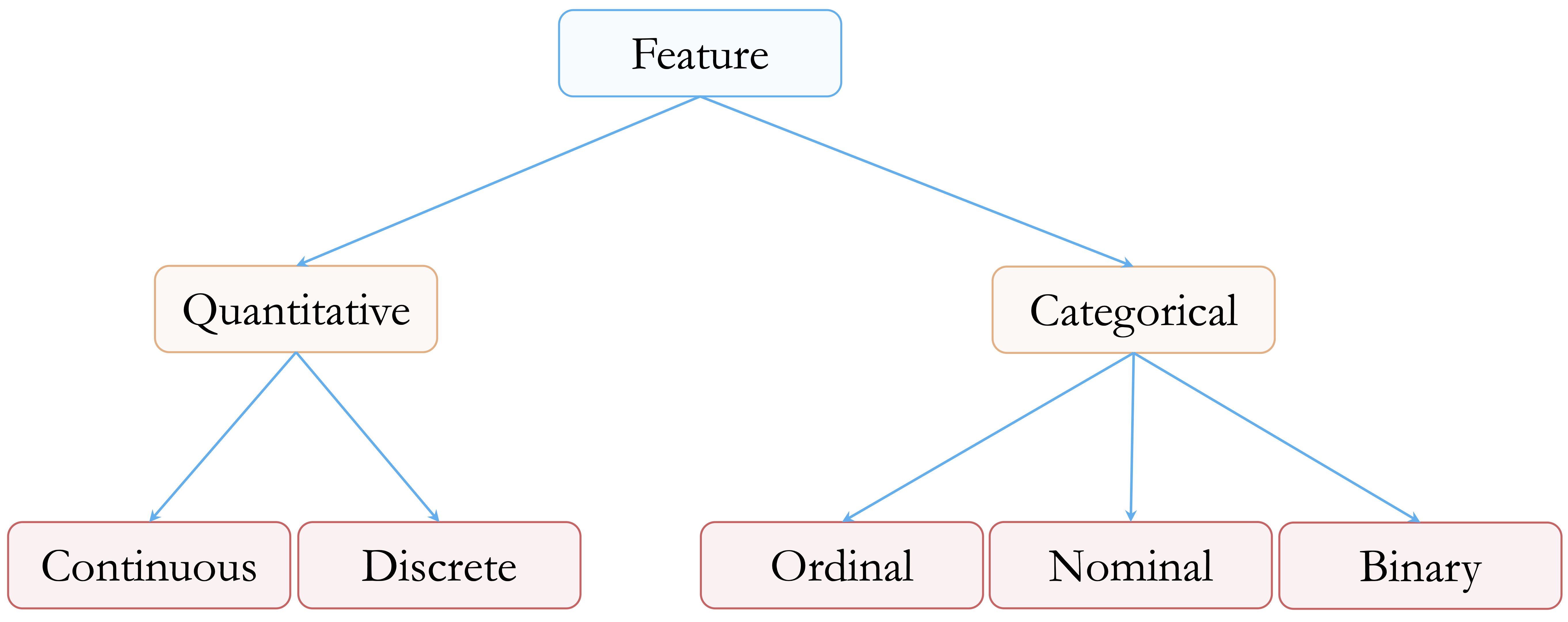
Features fall into two broad categories: quantitative (numerical) and categorical (qualitative), each with important subtypes.
Quantitative (Numerical) features represent measurable quantities:
Continuous features can take any value within a range. In the diamonds dataset, variables such as
carat,price,x,y,z, anddepthare continuous.Discrete features take on countable values, typically integers. Although not present in this dataset, an example might be the number of prior purchases or visits.
Categorical (Qualitative) features classify observations into groups:
Ordinal features have a meaningful order, though the spacing between levels is not necessarily equal. The diamonds dataset includes ordinal variables like
cut,color, andclarity. For example,colorranges from D to J, an alphabetical scale that reflects a progression from most to least colorless.Nominal features represent categories with no inherent order, such as product types or blood types.
Binary features have exactly two categories, such as “yes”/“no” or “male”/“female”, typically encoded as 0 and 1.
Although the diamonds dataset does not contain discrete, nominal, or binary features, these are frequently encountered in real-world datasets and require distinct handling strategies.
In R, how a variable is stored affects its treatment during analysis. Continuous variables are usually stored as numeric, while discrete ones are often integer. Categorical variables appear as factor objects, which may be either ordered or unordered. You can inspect these using str() for the full dataset, or use class() and typeof() to examine specific variables.
Tip: Always check how R interprets your variables. For example, a feature that is conceptually ordinal may be treated as a nominal
factorunless explicitly declared asordered = TRUE.
Now that we understand the structure of our features, we are ready to begin preparing them, starting with identifying outliers that may distort our analysis.
3.3 Key Considerations for Data Preparation
Effective data preparation serves as the bridge between raw input and meaningful statistical analysis. To prepare the diamonds dataset for modeling, we focus on three interrelated priorities: ensuring data quality, engineering relevant features, and transforming variables into suitable formats.
First, data quality is essential. We need to ensure that the dataset is accurate, consistent, and free from major issues. This includes identifying missing values, spotting outliers, and resolving inconsistencies that could introduce bias or reduce model performance.
Second, thoughtful feature engineering can add substantial value. For example, rather than using the x, y, and z dimensions separately, we might create a new variable that captures the volume of each diamond. This derived feature could serve as a more interpretable and effective predictor of price.
Finally, appropriate data transformation ensures that all features are in a format suitable for modeling. Categorical variables like cut or color need to be encoded numerically, using methods that respect their structure and meaning. At the same time, numerical features may require scaling to ensure they contribute fairly in algorithms that rely on distance or gradient-based optimization.
These three pillars—data quality, feature engineering, and transformation—form the foundation of robust data preparation and help ensure that our modeling efforts are grounded in clean, well-structured, and informative data.
3.4 Outliers: What They Are and Why They Matter
Outliers are observations that stand out from the general pattern of a dataset, extreme values that differ markedly from the rest. They can arise from data entry errors, unusual measurement conditions, or genuinely rare but meaningful events. Regardless of their source, outliers can have an outsized impact on data analysis: they may distort summary statistics, skew visualizations, and mislead machine learning models.
Recognizing and handling outliers appropriately is especially important in real-world applications. In finance, an unusually large transaction could indicate fraud. In healthcare, an extreme lab result might point to a rare diagnosis, or signal a faulty instrument. In manufacturing, sensor readings that deviate from the norm might flag equipment failure or process instability.
However, not all outliers are errors to be discarded. Some reflect valuable exceptions that offer new insights. Removing them indiscriminately risks throwing away useful information; keeping them blindly can undermine model reliability. Sound judgment, grounded in both statistical reasoning and domain knowledge, is essential when deciding how to handle them.
Outlier detection can begin with visual tools such as boxplots, histograms, and scatter plots, which offer intuitive ways to spot anomalies. These methods are especially useful during the exploratory phase of analysis. More formal techniques, such as z-scores and interquartile range (IQR) thresholds, provide quantitative criteria for identifying unusually high or low values.
In the next section, we apply visual tools to the diamonds dataset to see how outliers manifest in real data and how they might affect our understanding of key variables.
3.5 Spotting Outliers with Visual Tools
Visualization is often the most accessible and informative way to begin detecting outliers. It helps us identify values that stray far from the typical range, whether due to data entry mistakes, rare but valid events, or measurement anomalies. In this section, we apply visual methods to the y variable (diamond width) from the diamonds dataset, a feature known to contain extreme or implausible values that warrant closer inspection.
Boxplots: Visualizing and Flagging Outliers
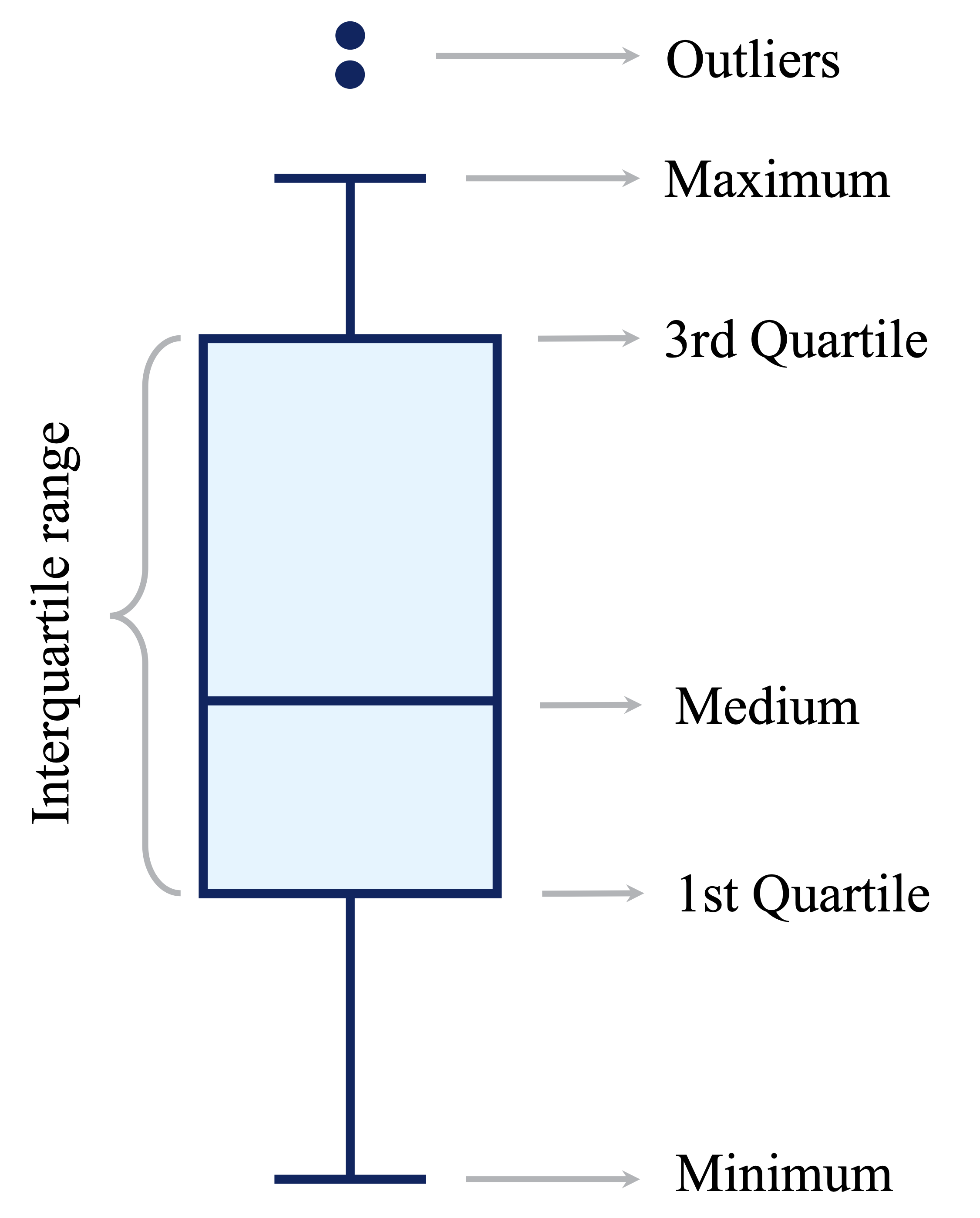
Boxplots provide a compact visual summary of a variable’s distribution. They highlight key statistics, such as the median and interquartile range (IQR), while flagging unusually high or low values as potential outliers. As shown in Figure 3.2, the “whiskers” extend to 1.5 times the IQR from the lower and upper quartiles, and data points beyond this range are considered outliers.
To see this in action, let us apply a boxplot to the y variable (diamond width) in the diamonds dataset:
ggplot(data = diamonds) +
geom_boxplot(mapping = aes(y = y))
ggplot(data = diamonds) +
geom_boxplot(mapping = aes(y = y)) +
coord_cartesian(ylim = c(0, 15))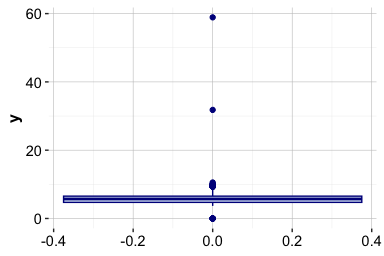
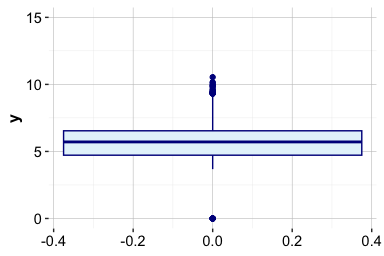
The left plot shows the full range of y values, where extreme observations above 15 mm compress the rest of the distribution and obscure the central pattern. The right plot zooms in on a more typical range (0–15 mm), revealing that most diamond widths fall between 2 and 6 mm, with a few clear outliers.
Boxplots like these allow us to quickly identify suspicious values, such as widths near 0 mm or above 15 mm, that are implausible for real diamonds. These anomalies may reflect data entry errors or rare but important cases that deserve closer inspection.
Histograms: Revealing Outlier Patterns
Histograms provide a complementary view to boxplots by showing how values are distributed across intervals. They reveal the overall shape of the distribution, highlight skewness, and help detect isolated spikes or rare values that may signal outliers.
The following histogram visualizes the distribution of the y variable (diamond width) using bins of width 0.5:
ggplot(data = diamonds) +
geom_histogram(aes(x = y), binwidth = 0.5)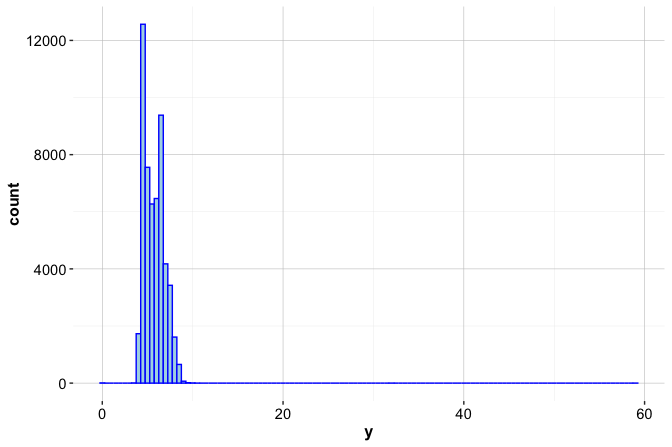
In this full-scale view, the concentration of values between 2 and 6 mm is clear, but less frequent values, especially those beyond 15 mm, are hard to see due to scale compression.
To focus on the rare and extreme cases, we zoom in on the lower portion of the frequency axis:
ggplot(data = diamonds) +
geom_histogram(mapping = aes(x = y), binwidth = 0.5) +
coord_cartesian(ylim = c(0, 30))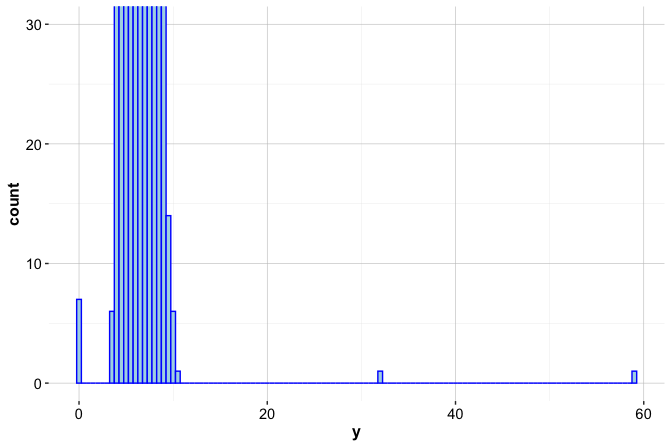
This refined view reinforces what we observed in the boxplot, namely, the presence of unusually small or large values in the y variable that fall outside the expected range. These may correspond to data entry errors or genuine anomalies, and they warrant closer inspection. Together with boxplots, histograms are powerful tools for identifying and interpreting potential outliers.
Additional Tools for Visual Outlier Detection
In addition to boxplots and histograms, several other visualization tools can help identify outliers in different contexts:
Violin plots combine the summary statistics of a boxplot with a mirrored density curve, offering insight into both distribution shape and the presence of extreme values.
Density plots provide a smoothed view of the data distribution, making it easier to detect long tails, multiple modes, or subtle irregularities.
Scatter plots are particularly useful for examining relationships between two variables and identifying outliers that deviate from general trends, especially in bivariate or multivariate contexts.
These tools are valuable in the early stages of analysis, when scanning for irregular patterns or unusual cases. However, as the number of dimensions increases, visual methods alone may no longer suffice. In such cases, formal statistical techniques, covered later in the book, offer more rigorous and scalable solutions for outlier detection.
Now that we have visually identified potential outliers, the next step is to decide how to handle them: whether to remove, transform, or retain these points based on their context and potential impact on analysis and modeling.
3.6 How to Handle Outliers
Why would a diamond have a width of 0 mm, or a price twenty times higher than its peers? Outliers like these appear in nearly every real-world dataset, and deciding what to do with them is a recurring challenge in data science. When guiding students through messy datasets, I often hear the same question: “Should I remove this outlier?” My advice is to pause and reflect. Not all outliers are errors, and not all errors are obvious.
Once outliers have been identified, either visually or statistically, the next step is to decide how to respond. There is no universal rule. The best course of action depends on whether the outlier reflects a data entry mistake, a rare but valid observation, or a meaningful signal. Context is critical, and decisions should be shaped by the modeling goals and the domain in which the data was collected.
Below are several practical strategies for handling outliers, each with its own trade-offs:
Retain the outlier if it is a valid observation that may contain valuable information. For instance, in fraud detection, statistical outliers often correspond to precisely the cases of interest. In the adult dataset, extreme values for
capital.gainmay reveal unique high-income individuals. Removing such observations could lead to a loss of predictive power or insight.Replace the outlier with a missing value when there is strong evidence that it is erroneous. For example, a negative carat weight or a repeated record likely stems from a data entry issue. Replacing such values with
NAallows for flexible downstream handling, including imputation strategies introduced in the next section.Flag and preserve the outlier by creating an indicator variable (e.g.,
is_outlier) to retain the observation without distorting the analysis. This is especially useful when the outlier might be informative but requires separate treatment.Apply data transformations, such as logarithmic or square root scaling, to reduce the influence of extreme values while preserving relative patterns.
Apply winsorization, which replaces extreme outlier values with less extreme percentile values (e.g., capping values at the 1st and 99th percentiles). This approach reduces the impact of outliers while retaining all observations, balancing robustness and data retention.
Use robust modeling techniques that are less sensitive to outliers. Decision trees, random forests, and median-based estimators are designed to accommodate variability without being unduly influenced by extreme points.
Remove the outlier only if the value is clearly invalid, cannot be reasonably corrected or imputed, and would otherwise compromise the integrity of the analysis. This should be considered a last resort, not the default action.
In general, a cautious and informed approach is best. Automatically removing all outliers is tempting, especially for beginners, but it risks discarding rare yet meaningful variation. A thoughtful strategy, grounded in domain knowledge and analytical objectives, ensures that data remains both clean and insightful.
3.7 Outlier Treatment in Action
Now that we have seen how to spot outliers, how should we handle them in practice? Let us walk through a hands-on example using the diamonds dataset. Take the y variable, which measures diamond width. As we saw earlier, some entries are clearly implausible, values equal to 0 or greater than 30 mm are unlikely for real diamonds and likely stem from data entry errors or measurement glitches.
To fix these values, we turn to the dplyr package, part of the tidyverse. It offers a powerful yet readable syntax for data manipulation. One of its core functions, mutate(), allows us to create or modify columns directly within a data frame. If dplyr is not yet installed, you can add it with install.packages("dplyr"). Then, load the package and apply the following transformation:
This command creates a new dataset, diamonds_2, by replacing suspicious y values with NA. The logic is simple: if y is 0 or greater than 30, it is replaced; otherwise, it is left unchanged. This kind of targeted replacement keeps the rest of the data intact while removing values likely to distort analysis.
To verify the update, summarize the variable:
summary(diamonds_2$y)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
3.680 4.720 5.710 5.734 6.540 10.540 9This summary confirms how many values were flagged and how the range has shifted. The extreme outliers no longer dominate the distribution, and we can now proceed with a cleaner variable.
Try it yourself: Repeat this process for the x and z variables, which represent length and depth. Do they contain similar implausible values? Replace any unusual values with NA, and use summary() to assess the results. Practicing this on multiple variables helps reinforce the principle that outlier treatment is part of an ongoing diagnostic mindset, not just a one-time fix.
In the next section, we will move on to the next step in the data preparation pipeline: how to impute missing values in a statistically informed way.
3.8 Missing Values: What They Are and Why They Matter
Missing values are not just blank entries—they are clues to a larger story in your dataset. Like a puzzle with missing pieces, incomplete data can hide important patterns, distort results, and mislead your models. Before drawing conclusions or fitting algorithms, it is essential to detect and handle missing data with care.
In R, missing values usually appear as NA, but in real-world datasets, they often hide behind special codes like -1, 999, or 99.9. These placeholder values are easy to miss, and if ignored, can quietly undermine your analysis. For instance, in the cereal dataset from the liver package (explored in Section 13.4), the calories variable uses -1 to indicate missing data. Similarly, in the bank marketing dataset (Section 12.6), the pday variable uses -1 to signal that a client was not contacted. Recognizing and recoding these special cases is a crucial first step.
As highlighted in the story of Abraham Wald (Section 2.4), missing data is not always random. Wald’s insight came from what he could not see, damage on planes that never returned. In data science, the absence of information can be just as telling as its presence. Overlooking this subtlety can lead to flawed assumptions and inaccurate models.
Students often ask, “How should we deal with missing values?” My advice is to avoid deleting data unless there is no alternative. While dropping incomplete rows is fast, it is rarely the best choice. In fact, if just 5% of values are missing across 30 variables, removing all rows with missing entries could eliminate up to 80% of your dataset. That is a steep price to pay. A more thoughtful approach, such as imputing missing values, preserves valuable information while supporting the goals of your analysis.
Broadly, there are two strategies for handling missing data:
Imputation involves estimating missing values using observed data. This method retains all records and helps maintain analytical completeness.
Removal excludes rows or columns with missing entries. While sometimes necessary, this approach can significantly shrink your dataset and introduce bias, especially if the missingness is not random.
In the following sections, we will explore how to identify missing values, understand their impact, and apply appropriate imputation techniques to create a more complete and trustworthy dataset.
3.9 Imputation Techniques
Once missing values have been identified, the next step is to choose an appropriate strategy for estimating them. The best method depends on the structure of the data, the analysis objectives, and how much complexity is acceptable. Below are several commonly used approaches:
Mean, median, or mode imputation replaces missing entries with the average (for numerical variables), median (for skewed distributions), or the most frequent category (for categorical variables). These simple methods are best suited for low levels of missingness and relatively uniform data.
Random sampling fills in missing values by drawing randomly from the observed values of the same variable. This technique preserves the variable’s distribution better than mean imputation but introduces randomness into the analysis.
Predictive imputation uses other variables in the dataset to estimate missing values through models such as linear regression, decision trees, or k-nearest neighbors. This approach is more accurate when strong relationships exist between variables.
Multiple imputation generates several completed datasets by repeating the imputation process multiple times and then combines results across them. This method accounts for uncertainty in the missing values and is especially useful for inference or reporting confidence intervals.
Selecting the right imputation method involves balancing simplicity and precision. For numerical variables with few missing entries, mean or median imputation often suffices. For categorical variables, mode imputation provides a straightforward alternative. In cases with substantial missingness or complex dependencies, predictive methods, such as regression or k-nearest neighbors, offer more reliable results. If a variable is missing too frequently, it may be better to exclude it or reconsider its role in the analysis.
In the coming example, we demonstrate the random sampling approach for its simplicity and illustrative value. However, in real-world applications, more advanced techniques are often preferred. Later in this chapter and in Chapter 13 (Section 13.4), we revisit this topic using Random Forest algorithm for imputation. This transition from basic to sophisticated methods reflects the increasing demands of applied data science.
Random Sampling Imputation in R
Let us now put imputation into practice using the y variable (diamond width) in the diamonds dataset. Earlier, we flagged implausible values, such as 0 or values above 30 mm, as missing (NA). Our goal here is to replace those missing values using random sampling, a simple technique that draws replacements from the observed, non-missing values of the same variable.
We use the impute() function from the Hmisc package, which supports several basic imputation strategies. If the package is not installed on your system, you can add it using install.packages("Hmisc"). Then, load the package and apply the imputation:
This command replaces each NA in the y column with a randomly selected value from the observed values, preserving the variable’s distribution. Because this technique introduces no systematic bias, it works well in exploratory settings where preserving the shape of the data is more important than prediction accuracy.
To assess the effect of imputation visually, the scatter plots below show the relationship between diamond width (y) and price before and after imputation:
ggplot(diamonds) +
geom_point(aes(x = y, y = price), size = 0.5, alpha = 0.6) +
labs(title = "With Outliers", x = "Diamond Size (y)", y = "Price")
ggplot(diamonds_2) +
geom_point(aes(x = y, y = price), size = 0.5, alpha = 0.6) +
labs(title = "After Imputation", x = "Diamond Size (y)", y = "Price") 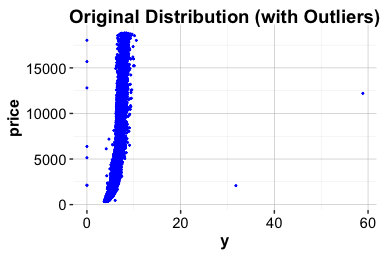
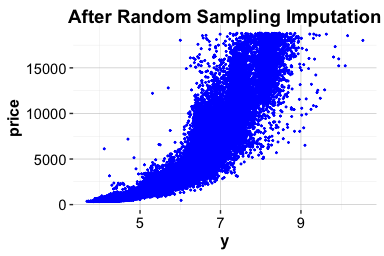
These plots illustrate that after removing implausible values and imputing missing entries, the data retains its overall structure while discarding extremes that could distort model training. Since price is our eventual target variable (see Chapter 10), this visualization also helps assess whether the cleaned y values still support meaningful patterns.
Try it yourself: Apply the same technique to the x and z variables, which represent diamond length and depth. First identify implausible values, recode them as NA, and then impute them using random sampling. Reflect on how these changes affect the variables’ relationships with price.
Other Imputation Approaches
The impute() function also supports several simple statistical methods, such as mean, median, and mode imputation. By default, it performs median imputation. For more flexible approaches, the aregImpute() function from Hmisc can be used. It performs predictive imputation using additive regression and bootstrapping, which often produces more realistic estimates than single-value replacements.
Another practical option is the mice (Multivariate Imputation by Chained Equations) package. Its mice() function performs multivariate imputation, modeling each variable with missing values as a function of the others in an iterative process. This method is particularly useful when multiple variables contain missing values that are correlated, as it accounts for their joint relationships and better reflects uncertainty in the imputations. In the case study in Chapter 13.4, we use the mice() function from the mice package to handle missing values in the cereal dataset, demonstrating its application in a realistic data preparation workflow.
Although removing missing records with na.omit() is quick and easy, it is generally discouraged unless a large portion of the data is missing or the missingness is systematic. Thoughtful imputation preserves valuable information and enhances the quality of subsequent analysis. In the next section, we bring together the methods introduced so far—handling missing values, addressing outliers, and cleaning inconsistent entries—in a hands-on case study that demonstrates how data preparation enables meaningful and trustworthy insights.
3.10 Case Study: Preparing Data to Predict High Earners
How can we determine whether a person earns more than $50,000 per year based on their demographic and occupational background? This question is relevant in many contexts, including economic research, policy evaluation, and the design of algorithmic hiring systems.
In this case study, we work with the adult dataset, originally derived from the US Census Bureau and made available through the liver package. The dataset contains variables such as age, education, marital status, occupation, and income, offering a rich basis for analysis.
Our goal is to predict whether an individual’s annual income exceeds $50,000. Later, in Chapter 11, we will revisit this dataset to construct predictive models with decision trees and random forests (see Section 11.5). At this stage, however, the emphasis is on preparing the data: handling missing values, encoding categorical variables, detecting outliers, and scaling numerical features so that the dataset is ready for modeling.
3.10.1 Overview of the Dataset
The adult dataset is a classic benchmark in machine learning, widely used for exploring income prediction based on demographic features. It reflects many of the data preparation challenges that analysts encounter in real-world applications.
To begin, let us load the adult dataset from the liver package. If you do not have the package installed, use the following command: install.packages("liver"). Then load the package and dataset:
To explore the dataset structure and data types, use the str() function:
str(adult)
'data.frame': 48598 obs. of 15 variables:
$ age : int 25 38 28 44 18 34 29 63 24 55 ...
$ workclass : Factor w/ 6 levels "?","Gov","Never-worked",..: 4 4 2 4 1 4 1 5 4 4 ...
$ demogweight : int 226802 89814 336951 160323 103497 198693 227026 104626 369667 104996 ...
$ education : Factor w/ 16 levels "10th","11th",..: 2 12 8 16 16 1 12 15 16 6 ...
$ education.num : int 7 9 12 10 10 6 9 15 10 4 ...
$ marital.status: Factor w/ 5 levels "Divorced","Married",..: 3 2 2 2 3 3 3 2 3 2 ...
$ occupation : Factor w/ 15 levels "?","Adm-clerical",..: 8 6 12 8 1 9 1 11 9 4 ...
$ relationship : Factor w/ 6 levels "Husband","Not-in-family",..: 4 1 1 1 4 2 5 1 5 1 ...
$ race : Factor w/ 5 levels "Amer-Indian-Eskimo",..: 3 5 5 3 5 5 3 5 5 5 ...
$ gender : Factor w/ 2 levels "Female","Male": 2 2 2 2 1 2 2 2 1 2 ...
$ capital.gain : int 0 0 0 7688 0 0 0 3103 0 0 ...
$ capital.loss : int 0 0 0 0 0 0 0 0 0 0 ...
$ hours.per.week: int 40 50 40 40 30 30 40 32 40 10 ...
$ native.country: Factor w/ 41 levels "?","Cambodia",..: 39 39 39 39 39 39 39 39 39 39 ...
$ income : Factor w/ 2 levels "<=50K",">50K": 1 1 2 2 1 1 1 2 1 1 ...The dataset contains 48598 observations and 15 variables. Most are predictors, while the target variable, income, indicates whether an individual earns more than $50,000 per year (>50K) or not (<=50K). The features include a mix of numerical and categorical variables, reflecting a range of demographic and economic attributes.
Below is a summary of the main variables:
-
age: Age in years (numerical); -
workclass: Employment type (categorical; 6 levels); -
demogweight: Census weighting factor (numerical); -
education: Highest educational attainment (categorical; 16 levels); -
education.num: Years of education (numerical); -
marital.status: Marital status (categorical; 5 levels); -
occupation: Job type (categorical; 15 levels); -
relationship: Household role (categorical; 6 levels); -
race: Racial background (categorical; 5 levels); -
gender: Gender identity (categorical; 2 levels); -
capital.gain: Annual capital gains (numerical); -
capital.loss: Annual capital losses (numerical); -
hours.per.week: Weekly working hours (numerical); -
native.country: Country of origin (categorical; 42 levels); -
income: Income bracket (<=50Kor>50K).
The dataset includes both numeric and categorical features, which we group as follows:
Numerical variables:
age,demogweight,education.num,capital.gain,capital.loss,hours.per.week.Binary variables:
gender,income.Ordinal variable:
education(ordered from “Preschool” to “Doctorate”).Nominal variables:
workclass,marital.status,occupation,relationship,race,native.country.
To better understand the dataset, use summary() to inspect distributions, detect possible anomalies, and identify missing values:
summary(adult)
age workclass demogweight education education.num marital.status
Min. :17.0 ? : 2794 Min. : 12285 HS-grad :15750 Min. : 1.00 Divorced : 6613
1st Qu.:28.0 Gov : 6536 1st Qu.: 117550 Some-college:10860 1st Qu.: 9.00 Married :22847
Median :37.0 Never-worked: 10 Median : 178215 Bachelors : 7962 Median :10.00 Never-married:16096
Mean :38.6 Private :33780 Mean : 189685 Masters : 2627 Mean :10.06 Separated : 1526
3rd Qu.:48.0 Self-emp : 5457 3rd Qu.: 237713 Assoc-voc : 2058 3rd Qu.:12.00 Widowed : 1516
Max. :90.0 Without-pay : 21 Max. :1490400 11th : 1812 Max. :16.00
(Other) : 7529
occupation relationship race gender capital.gain
Craft-repair : 6096 Husband :19537 Amer-Indian-Eskimo: 470 Female:16156 Min. : 0.0
Prof-specialty : 6071 Not-in-family :12546 Asian-Pac-Islander: 1504 Male :32442 1st Qu.: 0.0
Exec-managerial: 6019 Other-relative: 1506 Black : 4675 Median : 0.0
Adm-clerical : 5603 Own-child : 7577 Other : 403 Mean : 582.4
Sales : 5470 Unmarried : 5118 White :41546 3rd Qu.: 0.0
Other-service : 4920 Wife : 2314 Max. :41310.0
(Other) :14419
capital.loss hours.per.week native.country income
Min. : 0.00 Min. : 1.00 United-States:43613 <=50K:37155
1st Qu.: 0.00 1st Qu.:40.00 Mexico : 949 >50K :11443
Median : 0.00 Median :40.00 ? : 847
Mean : 87.94 Mean :40.37 Philippines : 292
3rd Qu.: 0.00 3rd Qu.:45.00 Germany : 206
Max. :4356.00 Max. :99.00 Puerto-Rico : 184
(Other) : 2507This summary provides a foundation for the next stages of data preparation: identifying missing values, detecting outliers, and encoding categorical features for modeling.
With a clear understanding of the dataset’s structure and variable types, we now begin the data preparation process. The first step is to detect and handle missing values, an essential task for ensuring the completeness and reliability of our analysis.
3.10.2 Handling Missing Values
A crucial early step in data preparation is identifying and resolving missing values. If left untreated, missing data can distort statistical summaries, reduce model accuracy, and bias conclusions.
The summary() function shows that three variables, workclass, occupation, and native.country, contain missing entries. In this dataset, however, missing values are not coded as NA, but as the string "?", a placeholder commonly used in public datasets such as those from the UCI Machine Learning Repository. Because R does not automatically recognize "?" as missing, we must recode it manually:
adult[adult == "?"] <- NAWe also apply droplevels() to remove unused categories from factor variables. This step helps prevent issues in later steps such as encoding:
adult <- droplevels(adult)To visualize the extent of missingness, we use the gg_miss_var() function from the naniar package. This function generates a bar chart showing the number and percentage of missing values per variable:
library(naniar)
gg_miss_var(adult, show_pct = TRUE)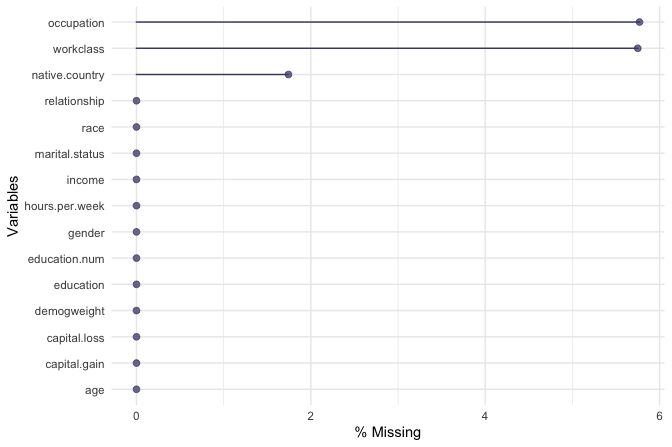
The resulting plot confirms that only three variables contain missing values: workclass with 2794 entries, occupation with 2804 entries, and native.country with 847 entries.
Since the proportion of missing values is small, less than 0.06% in each case, we choose to impute the missing values rather than remove rows, which could lead to information loss. To preserve each variable’s distribution, we use random imputation, which replaces missing entries by randomly sampling from observed (non-missing) values:
Finally, we recheck for missingness to confirm that the imputation succeeded:
gg_miss_var(adult, show_pct = TRUE)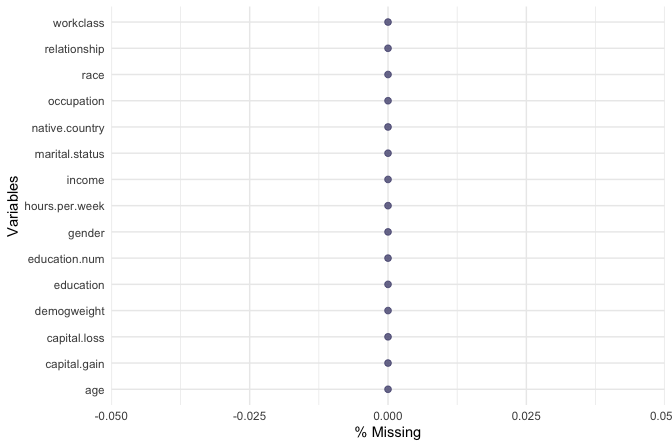
The updated plot should confirm that all missing values have been addressed. With this step complete, we are ready to prepare categorical features.
Preparing Categorical Features
Categorical features often contain many unique values, which can complicate analysis and make interpretation less clear. In the adult dataset, two features, native.country and workclass, have a relatively high number of categories. To simplify the analysis while preserving interpretability, we group related categories into broader, more informative classes.
Grouping native.country by Region
The native.country variable includes 40 distinct countries. Modeling each country as a separate category would unnecessarily expand the feature space and dilute predictive power. To improve interpretability and reduce sparsity, we group the countries into broader geographic regions that reflect cultural and linguistic proximity:
Europe: France, Germany, Greece, Hungary, Ireland, Italy, Netherlands, Poland, Portugal, United Kingdom, Yugoslavia.
North America: United States, Canada, Outlying US territories (Guam, US Virgin Islands, etc.).
Latin America: Mexico, El Salvador, Guatemala, Honduras, Nicaragua, Cuba, Dominican Republic, Puerto Rico, Colombia, Ecuador, Peru.
Caribbean: Jamaica, Haiti, Trinidad and Tobago.
Asia: Cambodia, China, Hong Kong, India, Iran, Japan, Laos, Philippines, South Korea (recorded as “South” in the dataset), Taiwan, Thailand, Vietnam.
The reclassification is performed using the fct_collapse() function from the forcats package. This function is designed for factor manipulation and allows you to combine multiple existing levels into broader, user-defined categories. It takes a factor variable as input and a set of named groups, where each name defines a new level and the associated vector lists the original levels to be merged. This approach keeps the factor variable tidy and avoids manual recoding.
library(forcats)
Europe <- c("France", "Germany", "Greece", "Hungary", "Ireland", "Italy", "Netherlands", "Poland", "Portugal", "United-Kingdom", "Yugoslavia")
North_America <- c("United-States", "Canada", "Outlying-US(Guam-USVI-etc)")
Latin_America <- c("Mexico", "El-Salvador", "Guatemala", "Honduras", "Nicaragua", "Cuba", "Dominican-Republic", "Puerto-Rico", "Colombia", "Ecuador", "Peru")
Caribbean <- c("Jamaica", "Haiti", "Trinidad&Tobago")
Asia <- c("Cambodia", "China", "Hong-Kong", "India", "Iran", "Japan", "Laos", "Philippines", "South", "Taiwan", "Thailand", "Vietnam")
adult$native.country <- fct_collapse(adult$native.country,
"Europe" = Europe,
"North America" = North_America,
"Latin America" = Latin_America,
"Caribbean" = Caribbean,
"Asia" = Asia
)To verify the transformation:
table(adult$native.country)
Asia North America Latin America Europe Caribbean
1108 44582 1899 797 212This regional grouping provides a balance between detail and interpretability. It retains key cultural and geographic distinctions (for example, between Latin America and the Caribbean) while minimizing sparsity and reducing the risk of overfitting when the variable is used in predictive modeling.
Simplifying workclass
The workclass variable categorizes employment types. Two of its levels, “Never-worked” and “Without-pay”, are rare and similar in nature, representing individuals outside formal employment. We consolidate these under a single label: Unemployed.
adult$workclass <- fct_collapse(adult$workclass, "Unemployed" = c("Never-worked", "Without-pay"))To confirm the update:
table(adult$workclass)
Gov Unemployed Private Self-emp
6919 32 35851 5796By reducing the number of categories in workclass and native.country, we streamline the dataset while retaining interpretability. This prepares the data for modeling algorithms that are sensitive to high-cardinality categorical inputs.
3.10.3 Handling Outliers
Identifying and addressing outliers is an important part of data preparation. Extreme values can distort summary statistics and influence the performance of models, particularly those sensitive to the range of numeric features. In this section, we focus on the capital.loss variable from the adult dataset to examine whether outliers are present and how they should be handled.
We begin with a basic summary:
summary(adult$capital.loss)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 0.00 0.00 87.94 0.00 4356.00From this output, we observe that the minimum value is 0, and the maximum is 4356. A majority of observations, over 75%, have a value of 0. The median, 0, is substantially lower than the mean, 87.94, indicating a right-skewed distribution influenced by high values.
To explore this further, we visualize the distribution using both a boxplot and a histogram:
ggplot(data = adult) +
geom_boxplot(aes(y = capital.loss)) +
ggtitle("Boxplot of Capital Loss")
ggplot(data = adult) +
geom_histogram(aes(x = capital.loss)) +
ggtitle("Histogram of Capital Loss")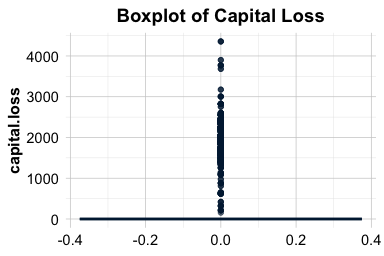
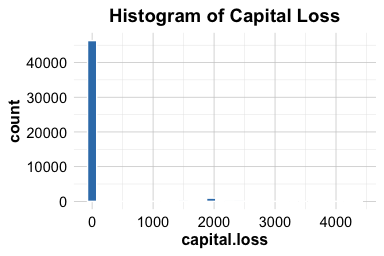
The boxplot shows a strong positive skew, with several high values extending beyond the upper whisker. The histogram confirms that most individuals report zero capital loss, with a few concentrated peaks near 2,000 and 4,000.
To focus more closely on the nonzero values, we restrict our analysis to rows where capital.loss > 0:
subset_adult <- subset(adult, capital.loss > 0)
ggplot(data = subset_adult) +
geom_boxplot(aes(y = capital.loss)) +
ggtitle("Boxplot of Nonzero Capital Loss")
ggplot(data = subset_adult) +
geom_histogram(aes(x = capital.loss)) +
ggtitle("Histogram of Nonzero Capital Loss")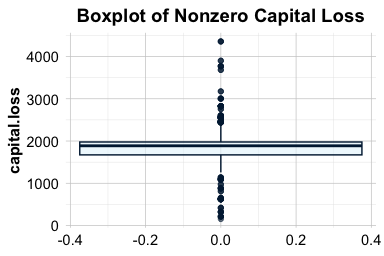
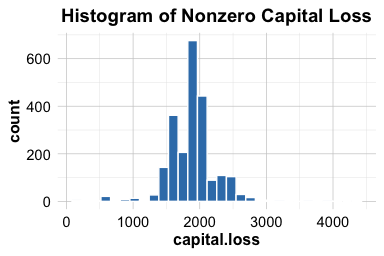
Among those with a nonzero capital loss, the majority of values are concentrated below 500. However, a small number of observations exceed 4,000. Despite their rarity, these high values appear to follow a relatively smooth and symmetric distribution, suggesting they reflect genuine variation in the data rather than data entry errors.
Given this context, we choose to retain the extreme values in capital.loss. They are likely to reflect meaningful differences across individuals and should not be removed without strong justification. If we later find that these values introduce problems for modeling, we may consider one of several strategies: applying a log or square-root transformation to reduce skewness, creating a binary variable to indicate whether a capital loss occurred, or using winsorization to cap extreme values at a defined threshold.
Understanding the structure of capital.loss also prepares us for handling the related variable capital.gain, which we explore next. For a hands-on example, see the guided exercise at the end of this chapter.
3.11 Chapter Summary and Takeaways
This chapter introduced the core steps of data preparation, focusing on how to transform raw and inconsistent data into a clean, reliable format suitable for analysis. Using the diamonds and adult datasets, we practiced identifying and managing outliers, detecting and imputing missing values, and resolving data inconsistencies.
We emphasized that data preparation is not merely a technical exercise but one guided by the structure and meaning of each feature. Outliers can distort relationships, missing values require thoughtful imputation, and inconsistent entries must be corrected to ensure interpretability and validity.
These techniques, though often overlooked, are essential for producing trustworthy insights and building models that reflect real patterns rather than noise. Clean, well-organized data forms the foundation of every effective data science project.
In the next chapter, we move from cleaning to exploring, using visualization and summary statistics to uncover patterns and relationships that guide our modeling choices.
3.12 Exercises
The exercises in this chapter are designed to strengthen both conceptual understanding and practical skills in data preparation. They move from foundational questions about data types and missingness to hands-on applications using the diamonds, adult, and housePrice datasets. Through these activities, you will practice identifying outliers, imputing missing values, and cleaning categorical features in real data contexts. The final self-reflection section encourages critical thinking about the role of data preparation in ensuring reliable, ethical, and interpretable analyses.
Conceptual Questions
Explain the difference between continuous and discrete numerical variables, and provide a real-world example of each.
Describe how ordinal and nominal categorical variables differ. Provide one example for each type.
Use the
typeof()andclass()functions in R to investigate how numerical and categorical variables are represented internally.Explain why it is important to identify the correct data types before modeling.
Discuss the advantages and disadvantages of removing outliers versus applying a transformation.
In a dataset where 25% of income values are missing, explain which imputation strategy you would use and justify your choice.
Define the difference between Missing Completely at Random (MCAR), Missing at Random (MAR), and Missing Not at Random (MNAR). Why is this distinction important for selecting an imputation method?
Explain why outlier detection should often be performed separately for numerical and categorical variables. Provide one example for each type.
Discuss how data preparation choices, such as imputation or outlier removal, can influence the fairness and interpretability of a predictive model.
Describe how reproducibility can be ensured during data preparation. What practices or tools in R help document cleaning and transformation steps effectively?
Hands-On Practice: Data Preparation for diamonds Dataset
Use
summary()to inspect the diamonds dataset. What patterns or irregularities do you observe?Classify all variables in the diamonds dataset as numerical, ordinal, or nominal.
Create histograms of
caratandprice. Describe their distributions and note any skewness or gaps.Identify outliers in the
xvariable using boxplots and histograms. If outliers are found, handle them using a method similar to the one applied toyin Section 3.4.Repeat the outlier detection process for the
zvariable and comment on the results.Examine the
depthvariable. Suggest an appropriate method to detect and address outliers in this case.Compute summary statistics for the variables
x,y, andzafter outlier handling. How do the results differ from the original summaries?Visualize the relationship between
caratandpriceusing a scatter plot. What pattern do you observe, and how might outliers influence it?Using the
dplyrpackage, create a new variable representing the volume of each diamond (x * y * z). Summarize and visualize this variable to detect any unrealistic or extreme values.
Hands-On Practice: Data Preparation for adult Dataset
Load the adult dataset from the liver package and classify its categorical variables as nominal or ordinal.
Compute the proportion of individuals earning more than $50K and interpret what this reveals about income distribution.
Create a boxplot and histogram of
capital.gain. Describe any patterns, anomalies, or extreme values.Identify outliers in
capital.gainand suggest an appropriate method for handling them.Compute and visualize a correlation matrix for the numerical variables. What do the correlations reveal about the relationships among features?
Use the
cut()function to groupageinto three categories: Young (\(\le 30\)), Middle-aged (31–50), and Senior (\(>50\)). Name the new variableAge_Group.Calculate the mean
capital.gainfor eachAge_Group. What trends do you observe?Create a binary variable indicating whether an individual has nonzero
capital.gain, and use it to produce an exploratory plot.Use
fct_collapse()to group the 16 education levels into broader categories. Propose at least three meaningful groupings and justify your choices.Define a new variable
net.capitalas the difference betweencapital.gainandcapital.loss. Visualize its distribution and comment on your findings.Investigate the relationship between
hours.per.weekand income level using boxplots or violin plots. What differences do you observe between income groups?Detect missing or undefined values in the
occupationvariable and replace them with an appropriate imputation method. Justify your choice.Examine whether combining certain rare
native.countrycategories (for example, by continent or region) improves interpretability without losing important variation. Discuss your reasoning.
Hands-On Practice: Data Preparation for housePrice Dataset
Load the housePrice dataset from the liver package. Identify variables with missing values and describe any observable patterns of missingness.
Detect outliers in
SalePriceusing boxplots and histograms. Discuss whether they appear to be data entry errors or meaningful extremes.Apply median imputation to one variable with missing data and comment on how the imputed values affect the summary statistics.
Suggest two or more improvements you would make to prepare this dataset for modeling.
Use the
skimrpackage (orsummary()) to generate an overview of all variables. Which variables may require transformation or grouping before modeling?Create a scatter plot of
GrLivAreaversusSalePrice. Identify any potential non-linear relationships or influential points that may warrant further investigation.Compute the correlation between
OverallQual,GrLivArea, andSalePrice. What insights do these relationships provide about property value drivers?Create a new categorical feature by grouping houses into price tiers (e.g., Low, Medium, High) based on quantiles of
SalePrice. Visualize the distribution ofOverallQualacross these groups and interpret your findings.
Self-Reflection
Explain how your approach to handling outliers might differ between patient temperature data and income data.
Consider a model that performs well in training but poorly in production. Reflect on how decisions made during data preparation could contribute to this discrepancy.
Reflect on a dataset you have worked with (or use the housePrice dataset). Which data preparation steps would you revise based on the techniques covered in this chapter?
Describe how data preparation choices, such as grouping categories or removing extreme values, can influence the fairness and interpretability of machine learning models.
Summarize the most important lesson you learned from working through this chapter’s exercises. How will it change the way you approach raw data in future projects?