6 Data Setup to Model

Prediction is very difficult, especially if it’s about the future.

— Niels Bohr

Suppose a churn prediction model reports 95% accuracy, yet consistently fails to identify customers who actually churn. What went wrong? In many cases, the issue lies not in the algorithm itself but in how the data was prepared for modeling. Before reliable machine learning models can be built, the dataset must be not only clean but also properly structured to support learning, validation, and generalization.

This chapter focuses on the fourth stage of the Data Science Workflow shown in Figure 2.3: Data Setup to Model. This stage involves organizing the dataset so that it enables fair training, trustworthy validation, and robust generalization to unseen data.

To accomplish this, we cover four essential tasks:

Partitioning: Splitting the dataset into training, validation, and testing subsets.
Validating: Ensuring that the subsets are representative of the overall data distribution.
Balancing: Addressing class imbalance when one category dominates in classification problems.
Feature Preparation: Encoding categorical variables and scaling numerical features.

The work in the previous chapters forms the foundation for this stage. In Section 2.4, you defined the modeling objective. In Chapter 3, you cleaned the data and handled issues such as missing values and outliers. Chapter Chapter 4 guided your exploratory analysis, and Chapter Chapter 5 introduced tools to test whether differences between datasets are statistically meaningful.

We now move to the modeling setup phase, a crucial but often underestimated step. It ensures that the data is not only clean but also statistically sound, well-structured, and ready for modeling. Proper data setup helps prevent common issues such as overfitting, biased evaluation, and data leakage, all of which can undermine model performance in practice.

This stage, particularly for newcomers, raises important questions: Why is it necessary to partition the data? How can we verify that training and test sets are truly comparable? What can we do if one class is severely underrepresented? When and how should we scale or encode features?

These are not just technical details; they reflect essential principles in modern data science—fairness, reproducibility, and trust. By walking through partitioning, validation, balancing, and feature preparation, we lay the groundwork for building models that not only perform well but also do so reliably and transparently in real-world settings.

What This Chapter Covers

This chapter completes Step 4 of the Data Science Workflow, Data Setup to Model. You will learn how to:

Partition a dataset into training and testing subsets to simulate deployment scenarios.
Validate that the data split is statistically representative and free from data leakage.
Address class imbalance using oversampling, undersampling, or class weighting techniques.
Scale numerical features with min–max and z-score methods to ensure comparability across predictors.
Encode categorical variables using ordinal, one-hot, and frequency encoding to make them compatible with machine learning algorithms.

By mastering these tasks, you will ensure that your data is not only clean but also properly structured for training machine learning models that are robust, fair, and generalizable.

6.1 Why Is It Necessary to Partition the Data?

For supervised learning, the first step in setting up data for modeling is to partition the dataset into training and testing subsets—a step often misunderstood by newcomers to data science. A common question is: Why split the data before modeling? The key reason is generalization, or the model’s ability to make accurate predictions on new, unseen data. This section explains why partitioning is essential for building models that perform well not only during training but also in real-world applications.

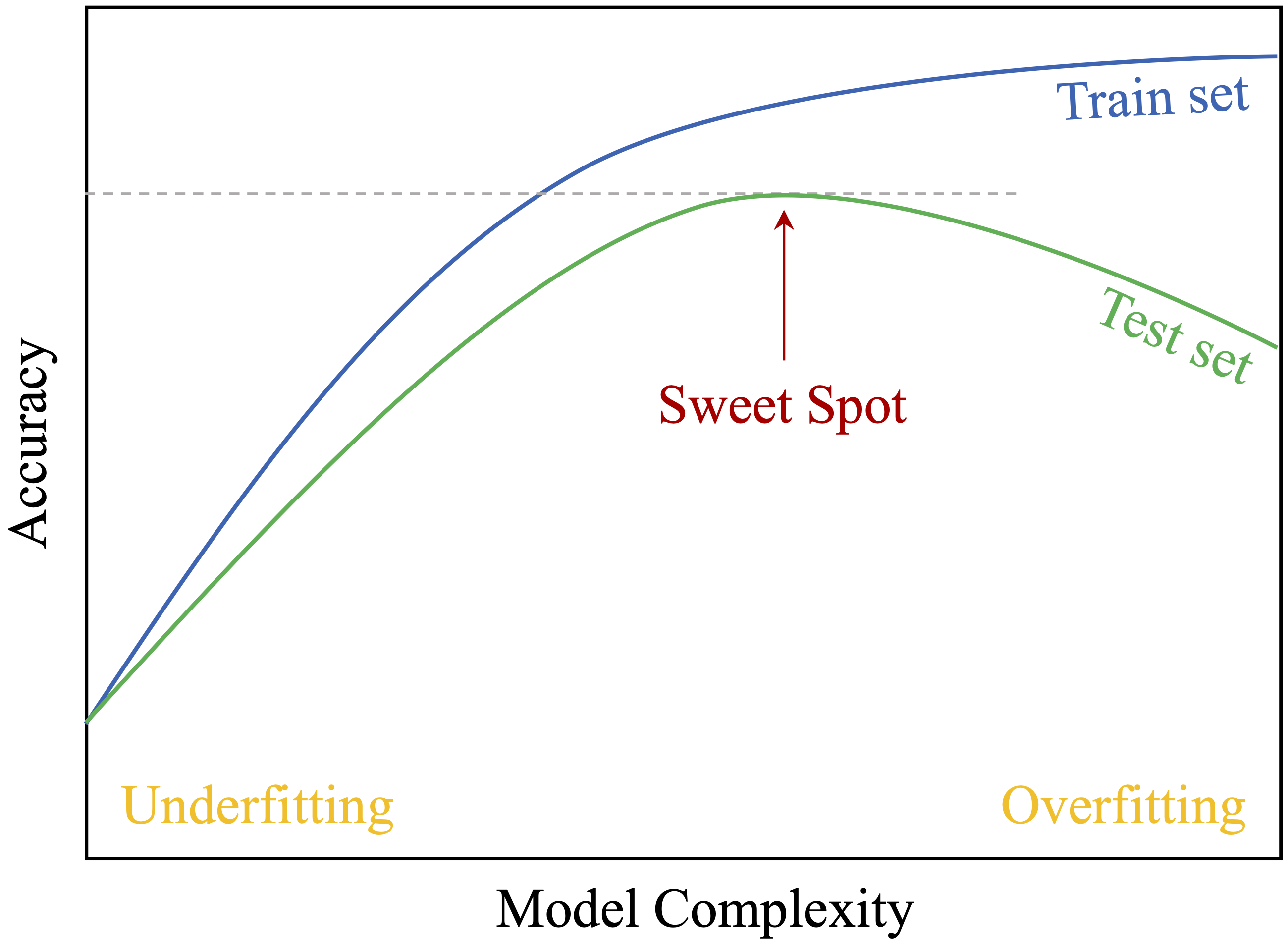
As part of Step 4 in the Data Science Workflow, partitioning precedes validation and class balancing. Dividing the data into a training set for model development and a test set for evaluation simulates real-world deployment. This practice guards against two key modeling pitfalls: overfitting and underfitting. Their trade-off is illustrated in Figure 6.1.

Figure 6.1: The trade-off between model complexity and accuracy on the training and test sets. Optimal performance is achieved at the point where test set accuracy is highest, before overfitting begins to dominate.

Overfitting occurs when a model captures noise and specific patterns in the training data rather than general trends. Such models perform well on training data but poorly on new observations. For instance, a churn model might rely on customer IDs rather than behavior, resulting in poor generalization.

Underfitting arises when the model is too simplistic to capture meaningful structure, often due to limited complexity or overly aggressive preprocessing. An underfitted model may assign nearly identical predictions across all customers, failing to reflect relevant differences.

Evaluating performance on a separate test set helps detect both issues. A large gap between high training accuracy and low test accuracy suggests overfitting, while low accuracy on both may indicate underfitting. In either case, model adjustments are needed to improve generalization.

Another critical reason for partitioning is to prevent data leakage, the inadvertent use of information from the test set during training. Leakage can produce overly optimistic performance estimates and undermine trust in the model. Strict separation of the training and test sets ensures that evaluation reflects a model’s true predictive capability on unseen data.

Figure 6.2 summarizes the typical modeling process in supervised learning:

Partition the dataset and validate the split.
Train models on the training data.
Evaluate model performance on the test data.

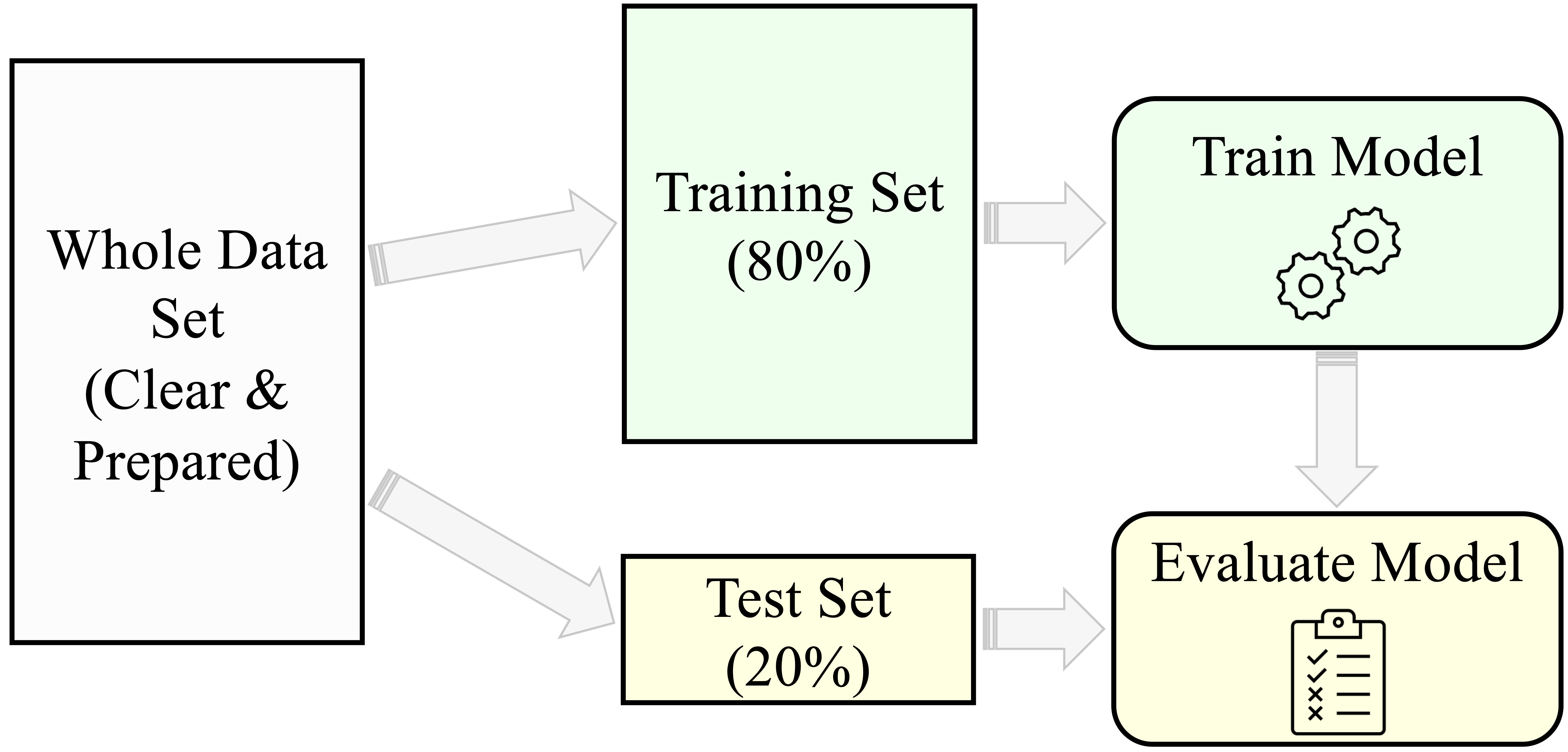
Figure 6.2: A general supervised learning process for building and evaluating predictive models. The 80–20 split ratio is a common default but may be adjusted based on the problem and dataset size.

By following this structure, we develop models that are both accurate and reliable. The remainder of this chapter addresses how to carry out each step in practice, beginning with partitioning strategies, followed by validation techniques and class balancing methods.

6.2 Partitioning Data: The Train–Test Split

Having established why partitioning is essential, we now turn to how it is implemented in practice. The most common method is the train–test split, also known as the holdout method. In this approach, the dataset is divided into two subsets: a training set used to develop the model and a test set reserved for evaluating the model’s ability to generalize to new, unseen data. This separation is essential for assessing out-of-sample performance.

Typical split ratios include 70–30, 80–20, or 90–10, depending on the dataset’s size and the modeling objectives. Both subsets include the same predictor variables and the outcome of interest, but only the training set’s outcome values are used during model fitting. The test set remains untouched during training to avoid data leakage and provides a realistic benchmark for evaluating the model’s predictive performance.

Example: Train–Test Split in R

We illustrate the train–test split using R and the liver package. We return to the churnCredit dataset introduced in Chapter 4.3, where the goal is to predict customer churn using machine learning models (discussed in the next chapter). First, following data preparation step in Section 4.3 we load and prepare the dataset as follows:

library(liver)

data(churnCredit)

churnCredit[churnCredit == "unknown"] <- NA
churnCredit <- droplevels(churnCredit)

library(Hmisc) 

churnCredit$education <- impute(churnCredit$education, "random")
churnCredit$income    <- impute(churnCredit$income, "random")
churnCredit$marital   <- impute(churnCredit$marital, "random")

The partition() function in the liver package provides a straightforward method to split a dataset based on a specified ratio. Below, we divide the dataset into 80% training and 20% test data:

set.seed(42)

data_sets = partition(data = churnCredit, ratio = c(0.8, 0.2))

train_set = data_sets$part1
test_set  = data_sets$part2

test_labels = test_set$churn

The use of set.seed(42) ensures reproducibility, meaning the same split will occur each time the code is run, a vital practice for ensuring reproducibility in model development and evaluation. The test_labels vector stores the actual target values from the test set and is used for evaluating model predictions. These labels must remain hidden during model training to avoid data leakage.

Splitting data into training and test sets allows us to assess a model’s generalization performance, that is, how well it predicts new, unseen data. While the train–test split is widely used, it can yield variable results depending on how the data is divided. A more robust and reliable alternative is cross-validation, introduced in the next section.

6.3 Cross-Validation for Robust Performance Estimation

While the train–test split is widely used for its simplicity, the resulting performance estimates can vary substantially depending on how the data is divided. Especially when working with smaller datasets. To obtain more stable and reliable estimates of a model’s generalization performance, cross-validation provides a valuable alternative.

Cross-validation is a resampling method that offers a more comprehensive evaluation than a single train–test split. In k-fold cross-validation, the dataset is randomly partitioned into k non-overlapping subsets (folds) of approximately equal size. The model is trained on k–1 folds and evaluated on the remaining fold. This process is repeated k times, with each fold serving once as the validation set. The overall performance is then estimated by averaging the metrics across all k iterations. Common choices for k include 5 or 10, as illustrated in Figure 6.3.

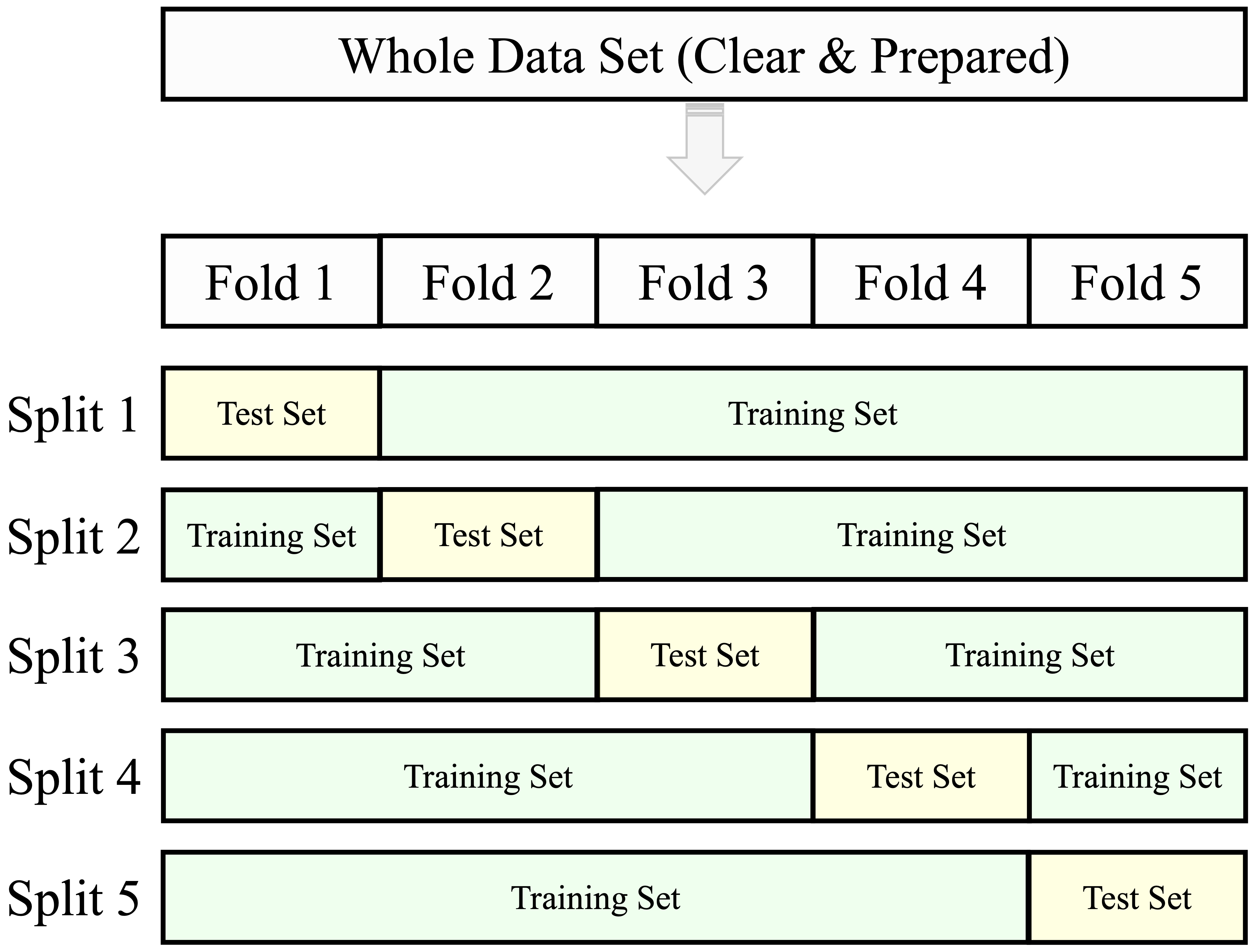
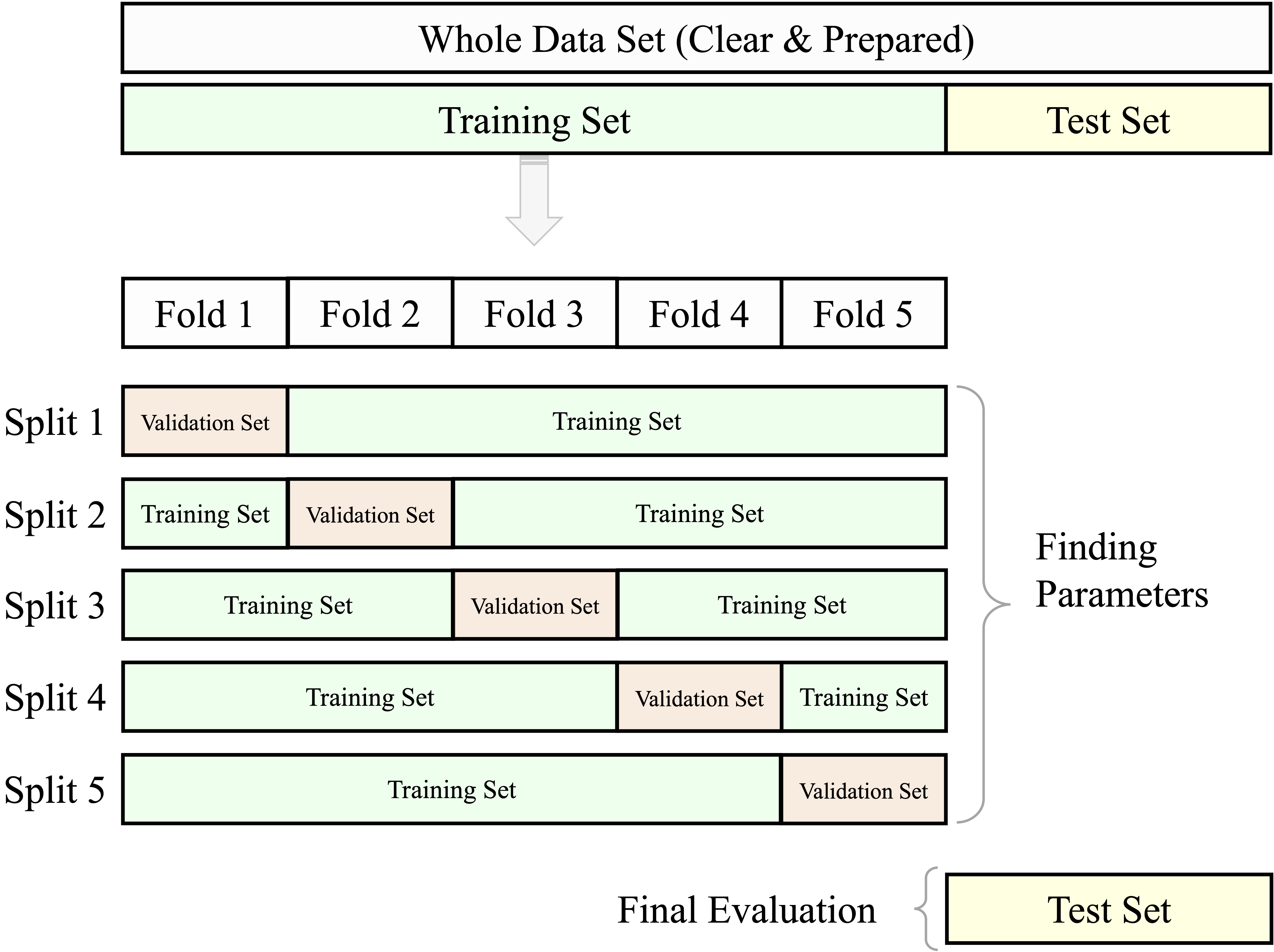
Figure 6.3: Illustration of k-fold cross-validation. The dataset is randomly split into k non-overlapping folds (k = 5 shown). In each iteration, the model is trained on k–1 folds (shown in green) and evaluated on the remaining fold (shown in yellow).

Cross-validation is especially useful for comparing models or tuning hyperparameters. However, repeated use of the test set during model development can lead to information leakage, resulting in overly optimistic performance estimates. To avoid this, it is best practice to hold out a separate test set for final evaluation, using cross-validation exclusively within the training set. In this setup, model selection and tuning rely on the cross-validated results from the training data, while the final model is evaluated once on the untouched test set.

This approach is depicted in Figure 6.4. It eliminates the need for a fixed validation subset and makes more efficient use of the training data, while preserving an unbiased test set for final performance reporting.

Figure 6.4: Cross-validation applied within the training set. The test set is held out for final evaluation only. This strategy eliminates the need for a separate validation set and maximizes the use of available data for both training and validation.

Although more computationally intensive, k-fold cross-validation helps reduce the variance of performance estimates and is particularly advantageous when data is limited. It ensures that evaluation reflects a model’s ability to generalize, rather than its performance on a specific data split. For further details and implementation examples, see Chapter 5 of An Introduction to Statistical Learning (James et al. 2013).

Partitioning data is a foundational step in predictive modeling. Yet even with a carefully designed split, it is important to verify whether the resulting subsets are representative of the original data. The next section addresses how to validate the quality of the partition before training begins.

6.4 How to Validate a Train-Test Split

How can we be sure that our train-test split truly represents the original dataset? After splitting the data, we must validate that the partition is statistically sound. A reliable split ensures that the training set reflects the broader population and that the test set mimics real-world deployment. Without this step, we risk building models that learn from biased data or fail to generalize.

Validation involves comparing the distributions of key variables, especially the target and influential predictors, across the training and testing sets. Since most datasets include many features, we usually focus on a subset that plays a central role in modeling. The statistical test we choose depends on the type of variable, as summarized in Table 6.1.

Table 6.1: Suggested hypothesis tests (from Chapter 5) for validating partitions, based on the type of target feature.

Type of Features	Suggested Test
Binary	Two-sample Z-test
Numerical	Two-sample t-test
Categorical (with \(> 2\) categories)	Chi-square test

Each test has specific assumptions. Parametric tests like the t-test and Z-test are most appropriate when sample sizes are large and distributions are approximately normal. For categorical features with more than two levels, the Chi-square test is the standard choice.

Let us illustrate this with the churn dataset by checking whether the proportion of churners is consistent across the training and testing sets. The target variable, churn (indicating whether a customer has churned), is binary. To determine whether the training and testing sets have similar churn rates, we conduct a two-sample Z-test. Thus, the hypotheses are defined as follows:

\[ \begin{cases} H_0: \pi_{\text{churn, train}} = \pi_{\text{churn, test}} \\ H_a: \pi_{\text{churn, train}} \neq \pi_{\text{churn, test}} \end{cases} \]

The R code below performs the test:

x1 <- sum(train_set$churn == "yes")
x2 <- sum(test_set$churn == "yes")

n1 <- nrow(train_set)
n2 <- nrow(test_set)

test_churn <- prop.test(x = c(x1, x2), n = c(n1, n2))
test_churn
   
    2-sample test for equality of proportions with continuity correction
   
   data:  c(x1, x2) out of c(n1, n2)
   X-squared = 0.045831, df = 1, p-value = 0.8305
   alternative hypothesis: two.sided
   95 percent confidence interval:
    -0.02051263  0.01598907
   sample estimates:
      prop 1    prop 2 
   0.1602074 0.1624691

Here, \(x_1\) and \(x_2\) denote the number of churners in the training and testing sets, respectively; \(n_1\) and \(n_2\) are the corresponding sample sizes. The function prop.test() performs the two-sample Z-test and returns a p-value indicating whether the difference in proportions is statistically significant.

The p-value is 0.83. Since this value is greater than the conventional significance level (\(\alpha = 0.05\)), we do not reject \(H_0\). This indicates that the observed difference in churn rates is not statistically significant, suggesting that the data split is valid with respect to the target variable.

Beyond the target variable, checking the distribution of key predictors helps detect imbalances that could bias the model. Unequal distributions in important features can lead the model to learn misleading or unrepresentative patterns. For instance, apply a two-sample t-test to compare means for numerical predictors such as age or available.credit, and use a Chi-square test for categorical variables like education. If available.credit is notably higher in the test set, a model trained on lower values may underpredict in deployment. Although it is rarely feasible to check every variable in high-dimensional datasets, focusing on known or selected predictors helps ensure a balanced and representative partition.

What If the Partition Is Invalid?

What should you do if the training and testing sets turn out to be significantly different? If validation reveals statistical imbalances, it is essential to take corrective steps to ensure that both subsets more accurately reflect the original dataset:

Revisit the random split: Even a random partition can result in imbalance due to chance. Try adjusting the random seed or modifying the split ratio to improve representativeness.
Use stratified sampling: This approach preserves the proportions of key categorical features, especially the target variable, across both training and test sets.
Apply cross-validation: Particularly valuable for small or imbalanced datasets, cross-validation reduces reliance on a single split and yields more stable performance estimates.

Even with careful attention, some imbalance may persist, especially in small or high-dimensional datasets. In such cases, additional techniques like bootstrapping or repeated sampling can improve stability and provide more reliable evaluations.

Remember, validation is more than a procedural checkpoint, it is a safeguard for the integrity of your modeling workflow. By ensuring that the training and test sets are representative, you enable models that learn honestly, perform reliably, and yield trustworthy insights. In the next section, we tackle another common issue: imbalanced classes in the training set.

6.5 Dealing with Class Imbalance

Imagine training a fraud detection model that labels every transaction as legitimate. It might boast 99% accuracy, yet fail completely at catching fraud. This scenario highlights the risk of class imbalance, where one class dominates the dataset and overshadows the rare but critical outcomes we aim to detect.

In many real-world classification tasks, one class is far less common than the other, a challenge known as class imbalance. This can lead to models that perform well on paper, often reporting high overall accuracy, while failing to identify the minority class. For example, in fraud detection, fraudulent cases are rare, and in churn prediction, most customers stay. If the model always predicts the majority class, it may appear accurate but will miss the cases that matter most.

Most machine learning algorithms optimize for overall accuracy, which can be misleading when the rare class is the true focus. A churn model trained on imbalanced data might predict nearly every customer as a non-churner, yielding high accuracy but missing actual churners, the very cases we care about. Addressing class imbalance is therefore an important step in setting up data for modeling, particularly when the minority class carries high business or scientific value.

Several strategies are commonly used to balance the training dataset and ensure that both classes are adequately represented during learning. Oversampling increases the number of minority class examples by duplicating existing cases or generating synthetic data. The popular SMOTE (Synthetic Minority Over-sampling Technique) method creates realistic synthetic examples instead of simple copies. Undersampling reduces the number of majority class examples by randomly removing observations and is useful when the dataset is large and contains redundant examples. Hybrid methods combine both approaches to achieve a balanced representation. Another powerful technique is class weighting, which adjusts the algorithm to penalize misclassification of the minority class more heavily. Many models, including logistic regression, decision trees, and support vector machines, support this approach natively.

These techniques must be applied only to the training set to avoid data leakage. The best choice depends on factors such as dataset size, the degree of imbalance, and the algorithm being used.

Let us walk through a concrete example using the churn dataset. The goal is to predict whether a customer has churned. First, we examine the distribution of the target variable in the training dataset:

# Check the class distribution
table(train_set$churn)
   
    yes   no 
   1298 6804

prop.table(table(train_set$churn))
   
         yes        no 
   0.1602074 0.8397926

The output shows that churners (churn = "yes") represent only a small proportion of the data, about 0.16, compared to non-churners. This class imbalance can result in a model that underemphasizes the very group we are most interested in predicting.

To address this in R, we can use the ovun.sample() function from the ROSE package to oversample the minority class so that it makes up 30% of the training set. This target ratio is illustrative; the optimal value depends on the use case and modeling goals.

If the ROSE package is not yet installed, use install.packages("ROSE").

# Load the ROSE package
library(ROSE)

# Oversample the training set to balance the classes with 30% churners
balanced_train_set <- ovun.sample(churn ~ ., data = train_set, method = "over", p = 0.3)$data

# Check the new class distribution
table(balanced_train_set$churn)
   
     no  yes 
   6804 2864
prop.table(table(balanced_train_set$churn))
   
         no      yes 
   0.703765 0.296235

The ovun.sample() function generates a new training set in which the minority class is oversampled to represent 30% of the data. The formula churn ~ . tells R to balance based on the target variable while keeping all predictors.

Always apply balancing after the data has been partitioned and only to the training set. Modifying the test set would introduce bias and make the model’s performance appear artificially better than it would be in deployment. This safeguard prevents data leakage and ensures honest evaluation.

Balancing is not always necessary. Many modern algorithms incorporate internal strategies for handling class imbalance, such as class weighting or ensemble techniques. These adjust the model to account for rare events without requiring explicit data manipulation. Furthermore, rather than relying solely on overall accuracy, evaluation metrics such as precision, recall, F1-score, and AUC-ROC offer more meaningful insights into model performance on imbalanced data. We will explore these evaluation metrics in more depth in Chapter 8, where we assess model performance under class imbalance.

In summary, dealing with class imbalance helps the model focus on the right outcomes and make more equitable predictions. It is a crucial preparatory step in classification workflows, particularly when the minority class holds the greatest value.

With class imbalance addressed, the next task is to prepare the predictors for modeling. Many datasets include categorical variables that must be converted into numerical form before they can be used by most machine learning algorithms. In the following section, we explore common strategies for encoding categorical features, followed by scaling methods for numerical variables to ensure consistent measurement across predictors.

6.6 Encoding Categorical Features

Categorical features often need to be transformed into numerical format before they can be used in machine learning models. Algorithms such as k-Nearest Neighbors and neural networks require numerical inputs, and failing to encode categorical data properly can lead to misleading results or even errors during model training.

Encoding categorical variables is a critical part of setting up data for modeling. It allows qualitative information—such as ratings, group memberships, or item types—to be incorporated into models that operate on numerical representations. In this section, we explore common encoding strategies and illustrate their use with examples from the churnCredit dataset, which includes the categorical variables marital and education.

The choice of encoding method depends on the nature of the categorical variable. For ordinal variables—those with an inherent ranking—ordinal encoding preserves the order of categories using numeric values. For example, the income variable in the churnCredit dataset ranges from <40K to >120K and benefits from ordinal encoding.

In contrast, nominal variables, which represent categories without intrinsic order, are better served by one-hot encoding. This approach creates binary indicators for each category and is particularly effective for features such as marital, where categories like married, single, and divorced are distinct but unordered.

The following subsections demonstrate these encoding techniques in practice, beginning with ordinal encoding and one-hot encoding. Together, these transformations ensure that categorical predictors are represented in a form that machine learning algorithms can interpret effectively.

6.7 Ordinal Encoding

For ordinal features with a meaningful ranking (such as low, medium, high), it is preferable to assign numeric values that reflect their order (e.g., low = 1, medium = 2, high = 3). This preserves the ordinal relationship in distance-based calculations, which would otherwise be lost with one-hot encoding.

Consider the income variable in the churnCredit dataset, which has levels <40K, 40K-60K, 60K-80K, 80K-120K, and >120K. We can convert this variable to numeric scores as follows:

# Convert an ordinal variable to numeric scores
churnCredit$income_level <- factor(churnCredit$income, 
                         levels = c("<40K", "40K-60K", "60K-80K", "80K-120K", ">120K"), 
                         labels = c(1, 2, 3, 4, 5))

churnCredit$income_level <- as.numeric(churnCredit$income_level)

If the feature were stored as a character variable, it should first be converted to a factor before applying this transformation:

churnCredit$income_level <- factor(churnCredit$income_level, 
                         levels = c("<40K", "40K-60K", "60K-80K", "80K-120K", ">120K"))

churnCredit$income_level <- as.numeric(churnCredit$income_level)

Both approaches ensure that the encoded values preserve the intended order of categories.

Try it yourself: Apply ordinal encoding to the cut variable in the diamonds dataset. The levels of cut are Fair, Good, Very Good, Premium, and Ideal. Assign numeric values from 1 to 5, reflecting their order from lowest to highest quality.

This transformation retains the ordinal structure and allows models that recognize ordered relationships—such as linear regression, decision trees, or ordinal logistic regression—to make more meaningful predictions.

However, ordinal encoding should only be applied when the order of categories is genuinely meaningful. Using it for nominal variables such as “red,” “green,” and “blue” would falsely imply a numerical hierarchy and could distort model interpretation and performance.

In summary, ordinal encoding is appropriate for variables with a natural ranking, where numerical values meaningfully represent category order. For variables without inherent order, a different approach is needed. The next section introduces one-hot encoding, a method designed specifically for nominal features.

6.8 One-Hot Encoding

How can we represent unordered categories, such as marital status, so that machine learning algorithms can use them effectively? One-hot encoding is a widely used solution. It transforms each unique category into a separate binary column, allowing algorithms to process categorical data without introducing an artificial order.

This method is particularly useful for nominal variables—categorical features with no inherent ranking. For example, the variable marital in the churnCredit dataset includes categories such as married, single, and divorced. One-hot encoding creates binary indicators for each category:

marital_married;
marital_single;
marital_divorced.

Each column indicates the presence (1) or absence (0) of a specific category. If there are \(k\) levels, only \(k - 1\) binary columns are required to avoid multicollinearity; the omitted category is implicitly represented when all others are zero.

Let us take a quick look at the marital variable in the churnCredit dataset:

table(churnCredit$marital)
   
    married   single divorced 
       5044     4275      808

The output shows the distribution of observations across the categories. We will now use one-hot encoding to convert these into model-ready binary features. This transformation ensures that all categories are represented without assuming any order or relationship among them.

One-hot encoding is essential for models that rely on distance metrics (e.g., k-nearest neighbors, neural networks) or for linear models that require numeric inputs.

6.8.1 One-Hot Encoding in R

To apply one-hot encoding in practice, we can use the one.hot() function from the liver package. This function automatically detects categorical variables and creates a new column for each unique level, converting them into binary indicators.

# One-hot encode the "marital" variable from the churnCredit dataset
churn_encoded <- one.hot(churnCredit, cols = c("marital"), dropCols = FALSE)

str(churn_encoded)
   'data.frame':    10127 obs. of  25 variables:
    $ customer.ID          : int  768805383 818770008 713982108 769911858 709106358 713061558 810347208 818906208 710930508 719661558 ...
    $ age                  : int  45 49 51 40 40 44 51 32 37 48 ...
    $ gender               : Factor w/ 2 levels "female","male": 2 1 2 1 2 2 2 2 2 2 ...
    $ education            : Factor w/ 6 levels "uneducated","highschool",..: 2 4 4 2 1 4 4 2 1 4 ...
     ..- attr(*, "imputed")= int [1:1519] 7 12 16 18 24 25 28 31 42 51 ...
    $ marital              : Factor w/ 3 levels "married","single",..: 1 2 1 2 1 1 1 1 2 2 ...
     ..- attr(*, "imputed")= int [1:749] 4 8 11 14 16 27 39 56 73 82 ...
    $ marital_married      : int  1 0 1 0 1 1 1 1 0 0 ...
    $ marital_single       : int  0 1 0 1 0 0 0 0 1 1 ...
    $ marital_divorced     : int  0 0 0 0 0 0 0 0 0 0 ...
    $ income               : Factor w/ 5 levels "<40K","40K-60K",..: 3 1 4 1 3 2 5 3 3 4 ...
     ..- attr(*, "imputed")= int [1:1112] 20 29 40 45 59 84 95 101 102 139 ...
    $ card.category        : Factor w/ 4 levels "blue","silver",..: 1 1 1 1 1 1 3 2 1 1 ...
    $ dependent.count      : int  3 5 3 4 3 2 4 0 3 2 ...
    $ months.on.book       : int  39 44 36 34 21 36 46 27 36 36 ...
    $ relationship.count   : int  5 6 4 3 5 3 6 2 5 6 ...
    $ months.inactive      : int  1 1 1 4 1 1 1 2 2 3 ...
    $ contacts.count.12    : int  3 2 0 1 0 2 3 2 0 3 ...
    $ credit.limit         : num  12691 8256 3418 3313 4716 ...
    $ revolving.balance    : int  777 864 0 2517 0 1247 2264 1396 2517 1677 ...
    $ available.credit     : num  11914 7392 3418 796 4716 ...
    $ transaction.amount.12: int  1144 1291 1887 1171 816 1088 1330 1538 1350 1441 ...
    $ transaction.count.12 : int  42 33 20 20 28 24 31 36 24 32 ...
    $ ratio.amount.Q4.Q1   : num  1.33 1.54 2.59 1.41 2.17 ...
    $ ratio.count.Q4.Q1    : num  1.62 3.71 2.33 2.33 2.5 ...
    $ utilization.ratio    : num  0.061 0.105 0 0.76 0 0.311 0.066 0.048 0.113 0.144 ...
    $ churn                : Factor w/ 2 levels "yes","no": 2 2 2 2 2 2 2 2 2 2 ...
    $ income_level         : num  3 1 4 1 3 2 5 3 3 4 ...

The cols argument specifies which variable(s) to encode. Setting dropCols = FALSE retains the original variable alongside the new binary columns; use TRUE to remove it after encoding. This transformation adds new columns such as marital_divorced, marital_married, and marital_single, each indicating whether a given observation belongs to that category.

Try it yourself: What happens if you encode multiple variables at once? Try applying one.hot() to both marital and card.category, and inspect the resulting structure.

While one-hot encoding is simple and effective, it can substantially increase the number of features, especially when applied to high-cardinality variables (e.g., zip codes or product names). Before encoding, consider whether the added dimensionality is manageable and whether all categories are meaningful for analysis.

Once categorical features are properly encoded, attention turns to numerical variables. These often differ in range and scale, which can affect model performance. The next section introduces feature scaling, a crucial step that ensures comparability across numeric predictors.

6.9 Feature Scaling

What happens when one variable, such as price in dollars, spans tens of thousands, while another, like carat weight, ranges only from 0 to 5? Without scaling, machine learning models that rely on distances or gradients may give disproportionate weight to features with larger numerical ranges, regardless of their actual importance.

Feature scaling addresses this imbalance by adjusting the range or distribution of numerical variables to make them comparable. It is particularly important for algorithms such as k-Nearest Neighbors (Chapter 7), support vector machines, and neural networks. Scaling can also improve optimization stability in models such as logistic regression and enhance the interpretability of coefficients.

In the churnCredit dataset, for example, available.credit ranges from 3 to 3.4516^{4}, while utilization.ratio spans from 0 to 0.999. Without scaling, features such as available.credit may dominate the learning process—not because they are more predictive, but simply because of their larger magnitude.

This section introduces two widely used scaling techniques:

Min–Max Scaling rescales values to a fixed range, typically \([0, 1]\).
Z-Score Scaling centers values at zero with a standard deviation of one.

Choosing between these methods depends on the modeling approach and the data structure. Min–max scaling is preferred when a fixed input range is required, such as in neural networks, whereas z-score scaling is more suitable for algorithms that assume standardized input distributions or rely on variance-sensitive optimization.

Scaling is not always necessary. Tree-based models, including decision trees and random forests, are scale-invariant and do not require rescaled inputs. However, for many other algorithms, scaling improves model performance, convergence speed, and fairness across features.

One caution: scaling can obscure real-world interpretability or exaggerate the influence of outliers, particularly when using min–max scaling. The choice of method should always reflect your modeling objectives and the characteristics of the dataset.

In the following sections, we demonstrate how to apply each technique in R using the churnCredit dataset. We begin with min–max scaling, a straightforward method for bringing all numerical variables into a consistent range.

6.10 Min–Max Scaling

When one feature ranges from 0 to 1 and another spans thousands, models that rely on distances—such as k-Nearest Neighbors—can become biased toward features with larger numerical scales. Min–max scaling addresses this by rescaling each feature to a common range, typically \([0, 1]\), so that no single variable dominates because of its units or magnitude.

The transformation is defined by the formula \[ x_{\text{scaled}} = \frac{x - x_{\text{min}}}{x_{\text{max}} - x_{\text{min}}}, \] where \(x\) is the original value and \(x_{\text{min}}\) and \(x_{\text{max}}\) are the minimum and maximum of the feature. This operation ensures that the smallest value becomes 0 and the largest becomes 1.

Min–max scaling is particularly useful for algorithms that depend on distance or gradient information, such as neural networks and support vector machines. However, this technique is sensitive to outliers: extreme values can stretch the scale, compressing the majority of observations into a narrow band and reducing the resolution for typical values.

To illustrate min–max scaling, consider the variable age in the churnCredit dataset, which ranges from approximately 26 to 73. We use the minmax() function from the liver package to rescale its values to the \([0, 1]\) interval:

ggplot(data = churnCredit) +
  geom_histogram(aes(x = age), bins = 15) +
  ggtitle("Before Min–Max Scaling")

ggplot(data = churnCredit) +
  geom_histogram(aes(x = minmax(age)), bins = 15) +
  ggtitle("After Min–Max Scaling")

The left panel shows the raw distribution of age, while the right panel displays the scaled version. After transformation, all values fall within the \([0, 1]\) range, making this feature numerically comparable to others—a crucial property when modeling techniques depend on distance or gradient magnitude.

While min–max scaling ensures all features fall within a fixed range, some algorithms perform better when variables are standardized around zero. The next section introduces z-score scaling, an alternative approach based on statistical standardization.

6.11 Z-Score Scaling

While min–max scaling rescales values into a fixed range, z-score scaling—also known as standardization—centers each numerical feature around zero and scales it to have unit variance. This technique is particularly useful for algorithms that assume normally distributed inputs or rely on gradient-based optimization, such as linear regression, logistic regression, and support vector machines.

The formula for z-score scaling is \[ x_{\text{scaled}} = \frac{x - \text{mean}(x)}{\text{sd}(x)}, \] where \(x\) is the original feature value, \(\text{mean}(x)\) is the mean of the feature, and \(\text{sd}(x)\) is its standard deviation. The result, \(x_{\text{scaled}}\), indicates how many standard deviations a given value is from the mean.

Z-score scaling places features with different units or magnitudes on a comparable scale. However, it remains sensitive to outliers, since both the mean and standard deviation can be influenced by extreme values.

To illustrate, let us apply z-score scaling to the age variable in the churnCredit dataset. The mean and standard deviation of age are approximately 46.33 and 8.02, respectively. We use the zscore() function from the liver package:

ggplot(data = churnCredit) +
  geom_histogram(aes(x = age), bins = 15) +
  ggtitle("Before Z-Score Scaling")

ggplot(data = churnCredit) +
  geom_histogram(aes(x = zscore(age)), bins = 15) +
  ggtitle("After Z-Score Scaling")

The left panel shows the original distribution of age values, while the right panel displays the standardized version, where values are centered around 0 and expressed in units of standard deviation. Although the location and scale are adjusted, the shape of the distribution—including any skewness—remains unchanged.

It is important to note that z-score scaling does not make a variable normally distributed. It standardizes the location and spread but preserves the underlying shape of the data. If a variable is skewed before scaling, it will remain skewed after transformation.

Preventing Data Leakage during Scaling

When applying feature scaling, it is essential to perform the transformation after partitioning the data. If scaling parameters (such as the mean, standard deviation, minimum, or maximum) are computed using the entire dataset before the split, information from the test set can inadvertently influence the training process—a phenomenon known as data leakage.

To prevent this, always fit the scaling transformation on the training set and then apply the same parameters to the test set. This ensures that the model is evaluated under true deployment conditions. A practical example of this principle is demonstrated in Section 7.5.1, where scaling is applied correctly in a k-Nearest Neighbors model.

With both categorical and numerical features now properly encoded and scaled, and with safeguards in place to prevent data leakage, the dataset is ready for modeling. The next section summarizes the key concepts and best practices introduced in this chapter.

6.12 Chapter Summary and Takeaways

This chapter completed Step 4 – Data Setup to Model in the Data Science Workflow, preparing the dataset for valid, generalizable, and trustworthy model development.

Partitioning data into training and testing sets was presented as a safeguard against overfitting and a means to simulate real-world prediction tasks.
Validating the train–test split ensured that both subsets were statistically representative, supporting reliable model evaluation.
Addressing class imbalance through techniques such as oversampling, undersampling, and class weighting improved model sensitivity to underrepresented outcomes.
Encoding categorical variables and scaling numerical features helped standardize data inputs, ensuring that all predictors contribute appropriately during model training.

Unlike other chapters in this book, this chapter does not include a dedicated case study. The techniques introduced here—partitioning, validation, balancing, and feature preparation—are integrated throughout the modeling chapters that follow. For instance, the churn classification case study in Section 7.7 demonstrates how these steps are applied in practice.

Together, these preparatory steps mitigate common risks such as biased evaluation, data leakage, and unfair comparisons between models. They provide a solid foundation for predictive modeling and ensure that model performance reflects genuine learning rather than artifacts of data structure. The next chapter builds on this foundation by introducing and evaluating classification models, beginning with k-Nearest Neighbors.

6.13 Exercises

This section combines conceptual questions and applied programming exercises designed to reinforce the key ideas introduced in this chapter. The goal is to consolidate essential preparatory steps for predictive modeling, focusing on partitioning, validating, balancing, and preparing features to support fair and generalizable learning.

Conceptual Questions

Why is partitioning the dataset crucial before training a machine learning model? Explain its role in ensuring generalization.
What is the main risk of training a model without separating the dataset into training and testing subsets? Provide an example where this could lead to misleading results.
Explain the difference between overfitting and underfitting. How does proper partitioning help address these issues?
Describe the role of the training set and the testing set in machine learning. Why should the test set remain unseen during model training?
What is data leakage, and how can it occur during data partitioning? Provide an example of a scenario where data leakage could lead to overly optimistic model performance.
Why is it necessary to validate the partition after splitting the dataset? What could go wrong if the training and test sets are significantly different?
How would you test whether numerical features, such as customer.calls in the churn dataset, have similar distributions in both the training and testing sets?
If a dataset is highly imbalanced, why might a model trained on it fail to generalize well? Provide an example from a real-world domain where class imbalance is a serious issue.
Why should balancing techniques be applied only to the training dataset and not to the test dataset?
Some machine learning algorithms are robust to class imbalance, while others require explicit handling of imbalance. Which types of models typically require class balancing, and which can handle imbalance naturally?
When dealing with class imbalance, why is accuracy not always the best metric to evaluate model performance? Which alternative metrics should be considered?
Suppose a dataset has a rare but critical class (e.g., fraud detection). What steps should be taken during the data partitioning and balancing phase to ensure effective model learning?
Why must categorical variables often be converted to numeric form before being used in machine learning models?
What is the key difference between ordinal and nominal categorical variables, and how does this difference determine the appropriate encoding technique?
Explain how one-hot encoding represents categorical variables and why this method avoids imposing artificial order on nominal features.
What is the main drawback of one-hot encoding when applied to variables with many categories (high cardinality)?
When is ordinal encoding preferred over one-hot encoding, and what risks arise if it is incorrectly applied to nominal variables?
Compare min–max scaling and z-score scaling. How do these transformations differ in their handling of outliers?
Why is it important to apply feature scaling after data partitioning rather than before?
What type of data leakage can occur if scaling is performed using both training and test sets simultaneously?

Hands-On Practice

The following exercises use the churn, bank, and risk datasets from the liver package. The churn and bank datasets were introduced earlier, while risk will be used again in Chapter 9.

library(liver)

data(churn)
data(bank)
data(risk)

Partitioning the Data

Partition the churn dataset into 75% training and 25% testing. Set a reproducible seed for consistency.
Perform a 90–10 split on the bank dataset. Report the number of observations in each subset.
Use stratified sampling to ensure that the churn rate is consistent across both subsets of the churn dataset.
Apply a 60–40 split to the risk dataset. Save the outputs as train_risk and test_risk.
Generate density plots to compare the distribution of income between the training and test sets in the bank dataset.

Validating the Partition

Use a two-sample Z-test to assess whether the churn proportion differs significantly between the training and test sets.
Apply a two-sample t-test to evaluate whether average age differs across subsets in the bank dataset.
Conduct a Chi-square test to assess whether the distribution of marital status differs between subsets in the bank dataset.
Suppose the churn proportion is 30% in training and 15% in testing. Identify an appropriate statistical test and propose a corrective strategy.
Select three numerical variables in the risk dataset and assess whether their distributions differ between the two subsets.

Balancing the Training Dataset

Examine the class distribution of churn in the training set and report the proportion of churners.
Apply random oversampling to increase the churner class to 40% of the training data using the ROSE package.
Use undersampling to equalize the deposit = "yes" and deposit = "no" classes in the training set of the bank dataset.
Create bar plots to compare the class distribution in the churn dataset before and after balancing.

Preparing Features for Modeling

Identify two categorical variables in the bank dataset. Decide whether each should be encoded using ordinal or one-hot encoding, and justify your choice.
Apply one-hot encoding to the marital variable in the bank dataset using the one.hot() function from the liver package. Display the resulting column names.
Perform ordinal encoding on the education variable in the bank dataset, ordering the levels from primary to tertiary. Confirm that the resulting values reflect the intended order.
Compare the number of variables in the dataset before and after applying one-hot encoding. How might this expansion affect model complexity and training time?
Apply min–max scaling to the numerical variables age and balance in the bank dataset using the minmax() function. Verify that all scaled values fall within the \([0, 1]\) range.
Use z-score scaling on the same variables with the zscore() function. Report the mean and standard deviation of each scaled variable and interpret the results.
In your own words, explain how scaling before partitioning could cause data leakage. Suggest a correct workflow for avoiding this issue (see Section 7.5.1).
Compare the histograms of one variable before and after applying z-score scaling. What stays the same, and what changes in the distribution?

Self-Reflection

Which of the three preparation steps—partitioning, validation, or balancing—currently feels most intuitive, and which would benefit from further practice? Explain your reasoning.
How does a deeper understanding of data setup influence your perception of model evaluation and fairness in predictive modeling?