4 Exploratory Data Analysis
The greatest value of a picture is when it forces us to notice what we never expected.
Exploratory Data Analysis (EDA) is the essential first step before building models or conducting statistical inference. It involves examining data carefully, thoroughly, and creatively to uncover insights. By revealing unexpected patterns, identifying anomalies, and highlighting potential relationships, EDA shapes the direction of all subsequent analysis.
EDA plays a pivotal role in the Data Science Workflow (see Figure 2.3), serving as the bridge between Data Preparation (Chapter 3) and Data Setup to Model (Chapter 6). This stage deepens our understanding of the data’s structure, quality, and potential, ensuring that downstream decisions rest on a solid empirical foundation.
Unlike formal hypothesis testing, EDA is not rigid or rule-driven. It is an iterative, open-ended process that encourages curiosity and experimentation. Different datasets raise different questions, and some exploratory paths will reveal meaningful trends while others uncover data issues or lead to dead ends. Through this process, analysts develop intuition, refine their focus, and identify the most informative features for modelling.
The purpose of EDA is not to confirm theories but to generate insight. Summary statistics, exploratory visualisations, and correlation measures provide an initial map of the data landscape. These findings should be interpreted cautiously, as early patterns may not represent causal relationships. In Chapter 5, we introduce formal tools for statistical inference that build on this exploratory foundation.
EDA also highlights the importance of practical relevance. In large datasets, weak patterns can easily reach statistical significance yet offer little real-world value. For example, a slight difference in customer engagement may be statistically detectable but too small to influence business decisions. Integrating domain expertise is therefore essential when interpreting exploratory findings.
Finally, EDA is central to assessing and improving data quality. Outliers, missing values, inconsistent formats, and redundant features often emerge during exploration. Addressing these issues early ensures that later models are both reliable and interpretable. The choice of EDA techniques depends on the nature of the data and the analytical questions at hand. Histograms and box plots reveal distributions, while scatter plots and correlation matrices expose relationships. The next sections introduce these tools in context and explain how to apply them effectively.
What This Chapter Covers
This chapter introduces exploratory data analysis as a critical stage in the data science workflow. You will learn how to use summary statistics and visual techniques to examine feature distributions, detect anomalies, and uncover relationships that inform downstream modelling. The chapter also shows how correlation analysis helps identify redundancy and how multivariate exploration can reveal patterns that enhance predictive insight.
The chapter begins with EDA as Data Storytelling, which emphasises the importance of communicating exploratory findings with clarity and context. This is followed by Key Objectives and Guiding Questions for EDA, which outline the main aims of exploration and the questions that support a structured analytical process.
Building on these ideas, the chapter presents a detailed exploration of the churnCredit dataset from the liver package. This example illustrates how real-world patterns emerge from data, how visualisations illuminate customer behaviour, and how exploratory insights prepare the ground for classification modelling using k-nearest neighbours in Chapter 7.
The chapter concludes with a comprehensive set of exercises and hands-on projects using two additional real-world datasets (bank and churn, also from the liver package). These activities provide further practice with EDA techniques and lay the foundation for the neural network case study in Chapter 12.
4.1 EDA as Data Storytelling
Exploratory data analysis is not only a technical process for uncovering patterns; it is also a way of communicating insights clearly and persuasively. While EDA reveals structure, anomalies, and relationships, these findings gain value only when they are presented with context and purpose. Data storytelling plays a central role in this process by transforming raw exploration into insight.
Effective storytelling in data science weaves together analytical evidence, contextual knowledge, and visual clarity. Rather than presenting statistics or plots in isolation, strong analysis connects each observation to a broader narrative. Whether the audience includes analysts, business stakeholders, or policymakers, the goal is to convey findings in a way that is meaningful and relevant.
Consider a typical observation: customers with high daytime usage appear more likely to churn. Stating this pattern is informative, but it does not yet offer understanding. A narrative that links the pattern to its implications brings the analysis to life:
“Customers with extensive daytime usage show a higher tendency to churn, possibly due to pricing concerns or dissatisfaction with service quality. Targeted retention strategies, such as customised discounts or more flexible pricing plans, may help address this risk.”
This shift from description to interpretation is at the heart of data storytelling. It invites reflection and supports informed decision-making.
Visualisation is central to this process. While summary statistics offer a structural overview, visual displays make patterns tangible. Scatter plots and correlation matrices highlight relationships among numerical features; histograms and box plots clarify distributions and skewness; bar charts and mosaic visualisations reveal differences across categories. Choosing appropriate visual tools not only strengthens analysis but also improves communication.
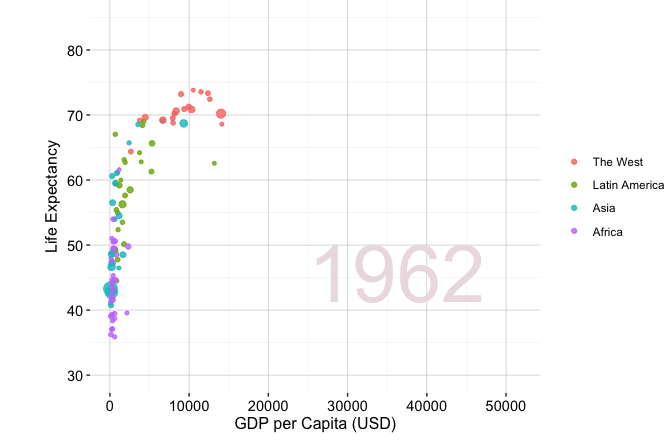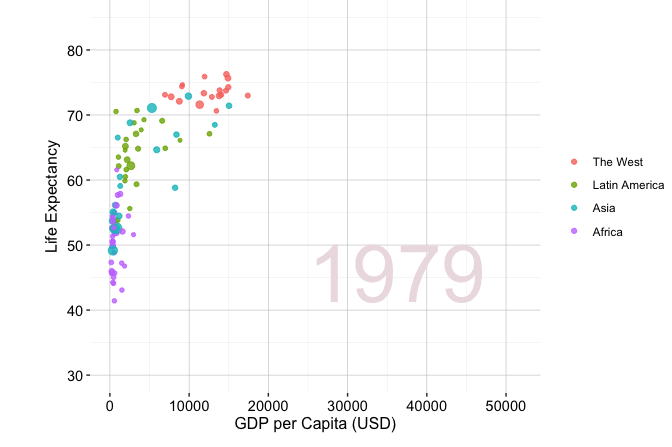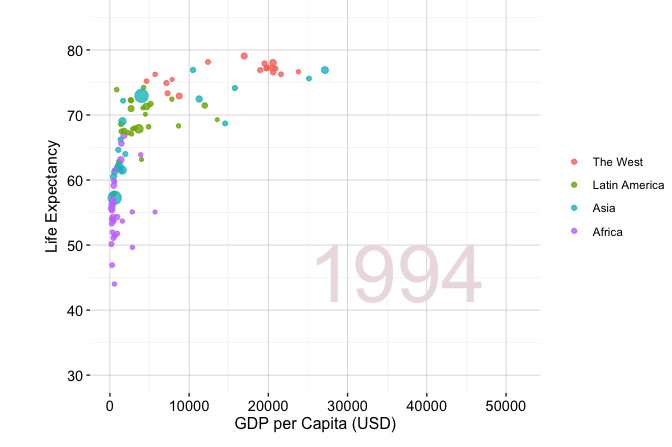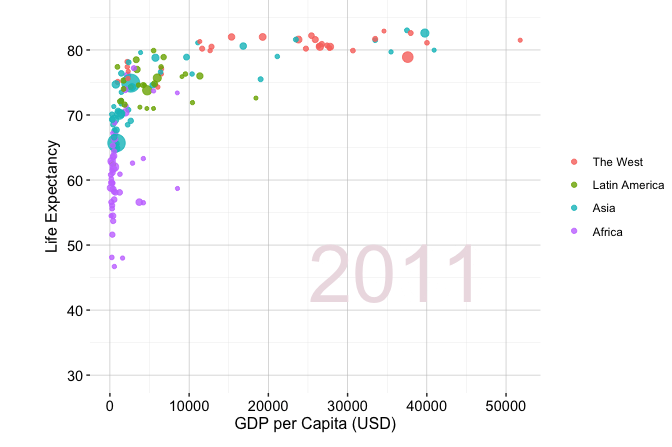
Storytelling through data is widely used across domains, from business and journalism to public policy and scientific research. A well-known example is Hans Rosling’s TED Talk New insights on poverty, where decades of demographic and economic data are presented in an engaging, intuitive format. Figure Figure 4.1, adapted from his presentation, illustrates how GDP per capita and life expectancy have changed across world regions from 1950 to 2019. The figure is generated from the gapminder dataset available in the liver package and visualised using ggplot2. Although drawn from global development, the same principles apply when exploring customer behaviour, financial trends, or service outcomes.

As you conduct EDA, it is useful to ask not only what the data shows, but also why those patterns matter. What story is emerging? How might that story inform a decision, challenge an assumption, or motivate further analysis? Thinking in narrative terms ensures that exploratory work is not merely descriptive but purposeful, rooted in the real-world questions that prompted the analysis.
The next section builds on these ideas by outlining the key objectives and guiding questions that shape effective exploratory analysis. Together, they provide a structured yet flexible foundation for the detailed EDA of customer churn that follows.
4.2 Objectives and Guiding Questions for EDA
EDA marks the first substantive interaction between analyst and dataset, the moment when raw information begins to reveal its structure, surprises, and potential narratives. Rather than moving directly into modelling, experienced analysts pause to ask what the data contains, which patterns stand out, and which issues require attention.
A useful starting point is to clarify what exploratory analysis is designed to accomplish. At its core, EDA seeks to understand the structure of the data, including feature types, value ranges, missing entries, and possible anomalies. It examines how individual features are distributed, identifying central tendencies, variation, and skewness. It investigates how features relate to one another, revealing associations, dependencies, or interactions that may later contribute to predictive models. It also detects patterns and outliers that might indicate errors, unusual subgroups, or emerging signals worth investigating further.
These objectives form the foundation for effective modelling. They help analysts refine which features deserve emphasis, anticipate potential challenges, and identify early insights that can guide the direction of later stages in the workflow.
Exploration becomes more productive when guided by focused questions. These questions can be grouped broadly into those concerning individual features and those concerning relationships among features. When examining features one at a time, the guiding questions ask what each feature reveals on its own, how it is distributed, whether missing values follow a particular pattern, and whether any irregularities stand out. Histograms, box plots, and summary statistics are familiar tools for answering such questions.
When shifting to relationships among features, the focus moves to how predictors relate to the target, whether any features are strongly correlated, whether redundancies or interactions might influence modelling, and how categorical and numerical features combine to reveal structure. Scatter plots, grouped visualisations, and correlation matrices help reveal these patterns and support thoughtful feature selection.
A recurring challenge, especially for students, is choosing which plots or techniques best suit different types of data. Table 4.1 summarises commonly used exploratory objectives alongside appropriate analytical tools. It serves as a practical reference when deciding how to approach unfamiliar datasets or new analytical questions.
| Exploratory.Objective | Applicable.Data.Type | Recommended.Techniques |
|---|---|---|
| Examine a feature’s distribution | Numerical | Histogram, box plot, density plot, summary statistics |
| Summarize a categorical feature | Categorical | Bar chart, frequency table |
| Identify outliers | Numerical | Box plot, histogram |
| Detect missing data patterns | Any | Summary statistics, missingness maps |
| Explore the relationship between two numerical features | Numerical & Numerical | Scatter plot, correlation coefficient |
| Compare a numerical feature across groups | Numerical & Categorical | Box plot, grouped bar chart, violin plot |
| Analyze interactions between two categorical features | Categorical & Categorical | Stacked bar chart, mosaic plot, contingency table |
| Assess correlation among multiple numerical features | Multiple Numerical | Correlation matrix, scatterplot matrix |
By aligning objectives with guiding questions and appropriate methods, EDA becomes more than a routine diagnostic stage. It becomes a strategic component of the workflow that enhances data quality, informs feature construction, and lays the groundwork for effective modelling.
The next section applies these principles through a detailed EDA of customer churn, showing how statistical summaries, visual tools, and domain understanding can uncover patterns that support predictive analysis.
4.3 EDA in Practice: The churnCredit Dataset
Exploratory data analysis (EDA) is most effective when it is grounded in real data and practical questions. In this section, we illustrate the process using the churnCredit dataset, which contains demographic, behavioural, and financial information about customers, together with a binary feature indicating whether each customer has churned (closed their credit card account).
This walkthrough follows the structure of the Data Science Workflow introduced in Chapter 2. We begin by revisiting the first two steps, Problem Understanding and Data Preparation, to clarify the business context and examine the structure of the dataset. The main focus is on Step 3: Exploratory Data Analysis, where visualisations, summary statistics, and guiding questions are used to uncover patterns related to customer churn.
The insights developed in this section provide a foundation for the subsequent stages of analysis: preparing the data for modelling in Chapter 6, constructing predictive models using k-nearest neighbours in Chapter 7, and assessing model performance in Chapter 8. Working through these stages in sequence demonstrates how a thorough exploratory analysis enhances understanding and supports well-founded decisions.
Problem Understanding for the churnCredit Dataset
A manager at a bank has become increasingly concerned about the rising number of customers closing their credit card accounts. Understanding why customers leave, and anticipating which customers are at risk of leaving, has become a strategic priority. Predicting churn would allow the bank to intervene proactively by offering improved services or incentives to retain valuable clients.
Customer churn is a persistent challenge in subscription-based industries such as banking, telecommunications, and streaming services. Because retaining existing customers is typically more cost-effective than acquiring new ones, identifying the factors that contribute to churn is a key task for analysts and decision-makers. From a business perspective, this problem gives rise to three central questions:
Why are customers choosing to leave?
Which behavioural or demographic characteristics are associated with higher churn risk?
How can these insights inform strategies designed to improve customer retention?
Exploratory data analysis provides an initial foundation for addressing these questions. By identifying patterns and relationships in the data, EDA uncovers early signals that can guide targeted retention initiatives. It also clarifies how customer attributes and behaviours interact, supporting later stages of predictive modelling.
In Chapter 7, a k-nearest neighbours (kNN) model will be developed to predict customer churn. Before building that model, it is necessary to understand the structure of the churnCredit dataset, the nature of its features, and the relationships they reveal. The next step therefore examines the dataset in detail to build this foundational understanding.
Overview of the churnCredit Dataset
Before conducting visual or statistical exploration, it is important to understand the dataset used throughout this chapter. The churnCredit dataset, available in the liver package, serves as a realistic case study for applying exploratory data analysis. It contains more than 10,000 customer records and 21 features that combine demographic information, account characteristics, credit usage, and customer interaction metrics.
The key feature of interest is churn, which indicates whether a customer has closed a credit card account (“yes”) or remained active (“no”). This binary outcome will later serve as the target feature for the classification model in Chapter 7. At this stage, the goal is to understand the structure, content, and quality of the data surrounding this outcome. To load and inspect the dataset, run:
library(liver)
data(churnCredit)
str(churnCredit)
'data.frame': 10127 obs. of 21 variables:
$ customer.ID : int 768805383 818770008 713982108 769911858 709106358 713061558 810347208 818906208 710930508 719661558 ...
$ age : int 45 49 51 40 40 44 51 32 37 48 ...
$ gender : Factor w/ 2 levels "female","male": 2 1 2 1 2 2 2 2 2 2 ...
$ education : Factor w/ 7 levels "uneducated","highschool",..: 2 4 4 2 1 4 7 2 1 4 ...
$ marital : Factor w/ 4 levels "married","single",..: 1 2 1 4 1 1 1 4 2 2 ...
$ income : Factor w/ 6 levels "<40K","40K-60K",..: 3 1 4 1 3 2 5 3 3 4 ...
$ card.category : Factor w/ 4 levels "blue","silver",..: 1 1 1 1 1 1 3 2 1 1 ...
$ dependent.count : int 3 5 3 4 3 2 4 0 3 2 ...
$ months.on.book : int 39 44 36 34 21 36 46 27 36 36 ...
$ relationship.count : int 5 6 4 3 5 3 6 2 5 6 ...
$ months.inactive : int 1 1 1 4 1 1 1 2 2 3 ...
$ contacts.count.12 : int 3 2 0 1 0 2 3 2 0 3 ...
$ credit.limit : num 12691 8256 3418 3313 4716 ...
$ revolving.balance : int 777 864 0 2517 0 1247 2264 1396 2517 1677 ...
$ available.credit : num 11914 7392 3418 796 4716 ...
$ transaction.amount.12: int 1144 1291 1887 1171 816 1088 1330 1538 1350 1441 ...
$ transaction.count.12 : int 42 33 20 20 28 24 31 36 24 32 ...
$ ratio.amount.Q4.Q1 : num 1.33 1.54 2.59 1.41 2.17 ...
$ ratio.count.Q4.Q1 : num 1.62 3.71 2.33 2.33 2.5 ...
$ utilization.ratio : num 0.061 0.105 0 0.76 0 0.311 0.066 0.048 0.113 0.144 ...
$ churn : Factor w/ 2 levels "yes","no": 2 2 2 2 2 2 2 2 2 2 ...The dataset is stored as a data.frame with 10127 observations and 21 features. The predictors consist of both numerical and categorical features that describe customer demographics, spending behaviour, credit management, and engagement with the bank. Eight features are categorical (gender, education, marital, income, card.category, churn, and two grouping identifiers), while the remaining features are numerical. The categorical features represent demographic or qualitative groupings, and the numerical features capture continuous measures such as credit limits, transaction amounts, and utilisation ratios. This distinction guides the choice of summary and visualisation techniques used later in the chapter.
A structured overview of the features is provided below:
-
customer.ID: Unique identifier for each account holder. -
age: Age of the customer, in years. -
gender: Gender of the account holder. -
education: Highest educational qualification. -
marital: Marital status. -
income: Annual income bracket. -
card.category: Credit card type (blue, silver, gold, platinum). -
dependent.count: Number of dependents. -
months.on.book: Tenure with the bank, in months. -
relationship.count: Number of products held by the customer. -
months.inactive: Number of inactive months in the past 12 months. -
contacts.count.12: Number of customer service contacts in the past 12 months. -
credit.limit: Total credit card limit. -
revolving.balance: Current revolving balance. -
available.credit: Unused portion of the credit limit, calculated ascredit.limit - revolving.balance. -
transaction.amount.12: Total transaction amount in the past 12 months. -
transaction.count.12: Total number of transactions in the past 12 months. -
ratio.amount.Q4.Q1: Ratio of total transaction amount in the fourth quarter to that in the first quarter. -
ratio.count.Q4.Q1: Ratio of total transaction count in the fourth quarter to that in the first quarter. -
utilization.ratio: Credit utilisation ratio, defined asrevolving.balance / credit.limit. -
churn: Whether the account was closed (“yes”) or remained active (“no”).
A first quantitative impression of the dataset can be obtained with:
summary(churnCredit)
customer.ID age gender education marital income card.category
Min. :708082083 Min. :26.00 female:5358 uneducated :1487 married :4687 <40K :3561 blue :9436
1st Qu.:713036770 1st Qu.:41.00 male :4769 highschool :2013 single :3943 40K-60K :1790 silver : 555
Median :717926358 Median :46.00 college :1013 divorced: 748 60K-80K :1402 gold : 116
Mean :739177606 Mean :46.33 graduate :3128 unknown : 749 80K-120K:1535 platinum: 20
3rd Qu.:773143533 3rd Qu.:52.00 post-graduate: 516 >120K : 727
Max. :828343083 Max. :73.00 doctorate : 451 unknown :1112
unknown :1519
dependent.count months.on.book relationship.count months.inactive contacts.count.12 credit.limit revolving.balance
Min. :0.000 Min. :13.00 Min. :1.000 Min. :0.000 Min. :0.000 Min. : 1438 Min. : 0
1st Qu.:1.000 1st Qu.:31.00 1st Qu.:3.000 1st Qu.:2.000 1st Qu.:2.000 1st Qu.: 2555 1st Qu.: 359
Median :2.000 Median :36.00 Median :4.000 Median :2.000 Median :2.000 Median : 4549 Median :1276
Mean :2.346 Mean :35.93 Mean :3.813 Mean :2.341 Mean :2.455 Mean : 8632 Mean :1163
3rd Qu.:3.000 3rd Qu.:40.00 3rd Qu.:5.000 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:11068 3rd Qu.:1784
Max. :5.000 Max. :56.00 Max. :6.000 Max. :6.000 Max. :6.000 Max. :34516 Max. :2517
available.credit transaction.amount.12 transaction.count.12 ratio.amount.Q4.Q1 ratio.count.Q4.Q1 utilization.ratio
Min. : 3 Min. : 510 Min. : 10.00 Min. :0.0000 Min. :0.0000 Min. :0.0000
1st Qu.: 1324 1st Qu.: 2156 1st Qu.: 45.00 1st Qu.:0.6310 1st Qu.:0.5820 1st Qu.:0.0230
Median : 3474 Median : 3899 Median : 67.00 Median :0.7360 Median :0.7020 Median :0.1760
Mean : 7469 Mean : 4404 Mean : 64.86 Mean :0.7599 Mean :0.7122 Mean :0.2749
3rd Qu.: 9859 3rd Qu.: 4741 3rd Qu.: 81.00 3rd Qu.:0.8590 3rd Qu.:0.8180 3rd Qu.:0.5030
Max. :34516 Max. :18484 Max. :139.00 Max. :3.3970 Max. :3.7140 Max. :0.9990
churn
yes:1627
no :8500
The summary statistics reveal several broad patterns:
Demographics and tenure: Customers are primarily middle-aged, with an average age of about 46 years, and have held their accounts for approximately three years.
Credit behaviour: Credit limits vary widely around an average of roughly 8,600 dollars. Available credit closely mirrors the credit limit, and utilisation ratios range from very low to very high, indicating a mix of conservative and heavy users.
Transaction activity: Customers complete about 65 transactions per year on average, with total annual spending near 4,400 dollars. The upper quartile contains high spenders whose behaviour may influence churn.
Behavioural changes: Quarterly spending ratios show a slight decline from the first to the fourth quarter for many customers, although some increase their spending.
Categorical features: Females form a slight majority. Education levels are concentrated in the college and graduate categories, and income tends to fall in lower brackets. Most customers hold blue cards, which reflects typical portfolio distributions.
These descriptive patterns illustrate the heterogeneity of the customer base and suggest that several numerical features may require scaling or transformation. Some categorical features, particularly education, marital, and income, contain an “unknown” category that represents missing information. Handling these cases is an important preparatory step.
The next subsection focuses on preparing the dataset for exploration by addressing missing values, verifying feature types, and ensuring consistent formats. Proper preparation ensures that the insights drawn from exploratory data analysis are both valid and interpretable.
Data Preparation for the churnCredit Dataset
The initial inspection of the churnCredit dataset revealed several data quality issues that need attention before beginning exploratory data analysis. Several categorical features (education, income, and marital) contain missing entries that were encoded as “unknown”. Replacing these placeholders with standard missing values is an important first step toward ensuring that summaries and visualisations accurately reflect the underlying data.
To standardise the representation of missing values, all “unknown” entries are converted to NA, and unused factor levels are removed:
churnCredit[churnCredit == "unknown"] <- NA
churnCredit <- droplevels(churnCredit)Before deciding how to handle missing values, it is helpful to assess their extent. The naniar package provides convenient tools for visualising missingness. The function gg_miss_var() displays the proportion of missing observations for each feature:
library(naniar)
gg_miss_var(churnCredit, show_pct = TRUE)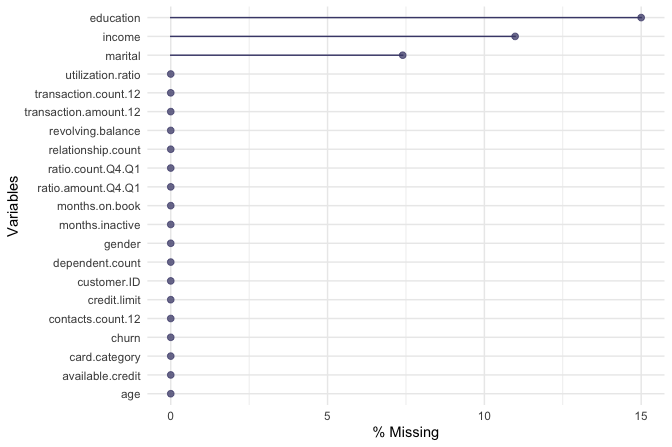
The plot shows that three categorical features (education, income, and marital) contain missing values, with the highest proportion appearing in education. Although the overall level of missingness is modest, resolving these cases is important to maintain consistency across groups.
Several approaches exist for imputing missing categorical values, including mode imputation, random assignment, or creating a separate category. Mode imputation would inflate the most common category, which could distort comparisons. A separate category would treat missingness as informative, which is not appropriate in this context. Random imputation preserves the original distribution of each feature, making it a suitable choice here. We use the function impute() from the Hmisc package:
After imputing missing values, it is good practice to verify that the data types of all features are correct. Categorical features should be stored as factors, and numerical features should be numeric, to ensure that later summaries and visualisations behave as expected:
str(churnCredit)
'data.frame': 10127 obs. of 21 variables:
$ customer.ID : int 768805383 818770008 713982108 769911858 709106358 713061558 810347208 818906208 710930508 719661558 ...
$ age : int 45 49 51 40 40 44 51 32 37 48 ...
$ gender : Factor w/ 2 levels "female","male": 2 1 2 1 2 2 2 2 2 2 ...
$ education : Factor w/ 6 levels "uneducated","highschool",..: 2 4 4 2 1 4 4 2 1 4 ...
..- attr(*, "imputed")= int [1:1519] 7 12 16 18 24 25 28 31 42 51 ...
$ marital : Factor w/ 3 levels "married","single",..: 1 2 1 2 1 1 1 1 2 2 ...
..- attr(*, "imputed")= int [1:749] 4 8 11 14 16 27 39 56 73 82 ...
$ income : Factor w/ 5 levels "<40K","40K-60K",..: 3 1 4 1 3 2 5 3 3 4 ...
..- attr(*, "imputed")= int [1:1112] 20 29 40 45 59 84 95 101 102 139 ...
$ card.category : Factor w/ 4 levels "blue","silver",..: 1 1 1 1 1 1 3 2 1 1 ...
$ dependent.count : int 3 5 3 4 3 2 4 0 3 2 ...
$ months.on.book : int 39 44 36 34 21 36 46 27 36 36 ...
$ relationship.count : int 5 6 4 3 5 3 6 2 5 6 ...
$ months.inactive : int 1 1 1 4 1 1 1 2 2 3 ...
$ contacts.count.12 : int 3 2 0 1 0 2 3 2 0 3 ...
$ credit.limit : num 12691 8256 3418 3313 4716 ...
$ revolving.balance : int 777 864 0 2517 0 1247 2264 1396 2517 1677 ...
$ available.credit : num 11914 7392 3418 796 4716 ...
$ transaction.amount.12: int 1144 1291 1887 1171 816 1088 1330 1538 1350 1441 ...
$ transaction.count.12 : int 42 33 20 20 28 24 31 36 24 32 ...
$ ratio.amount.Q4.Q1 : num 1.33 1.54 2.59 1.41 2.17 ...
$ ratio.count.Q4.Q1 : num 1.62 3.71 2.33 2.33 2.5 ...
$ utilization.ratio : num 0.061 0.105 0 0.76 0 0.311 0.066 0.048 0.113 0.144 ...
$ churn : Factor w/ 2 levels "yes","no": 2 2 2 2 2 2 2 2 2 2 ...With missing values addressed and feature types confirmed, the dataset is ready for exploratory analysis. The following section applies visual and numerical tools to uncover the key patterns that help explain customer churn.
4.4 Exploring Categorical Features
Categorical features group observations into distinct classes that often reflect demographic or behavioural characteristics. In the churnCredit dataset, key categorical features include gender, education, marital, card.category, and churn. Examining how these features are distributed, and how they relate to the outcome churn, provides an initial understanding of customer loyalty and disengagement.
We begin with the distribution of the target feature churn, which indicates whether a customer has closed a credit card account. Understanding this distribution is essential for assessing class balance, a factor that directly affects model training and interpretation. The bar plot and pie chart below summarise the proportion of customers who churned:
library(ggplot2)
# Bar plot
ggplot(data = churnCredit, aes(x = churn, label = scales::percent(prop.table(after_stat(count))))) +
geom_bar(fill = c("#F4A582", "#A8D5BA")) +
geom_text(stat = "count", vjust = 0.4, size = 6)
# Pie chart
ggplot(churnCredit, aes(x = "", fill = churn)) +
geom_bar(width = 1) +
coord_polar(theta = "y") +
theme_void()
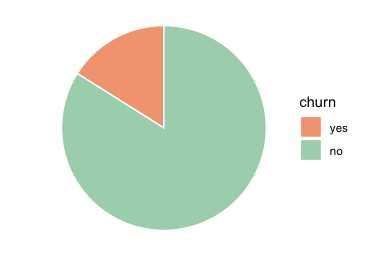
The left panel shows the bar plot, while the right panel presents a pie chart of the same proportions. Both highlight that most customers remain active (churn = "no"), with only a small proportion (about 16.1 percent) closing their accounts. Although pie charts are less useful for multi-category comparisons, they can be effective for summarising a single binary feature such as churn.
A simpler bar plot without colours or percentage labels can be created with:
The basic version provides a quick overview of class counts, whereas the enhanced plot conveys proportions more clearly. Such refinements improve interpretability when communicating results to non-technical audiences.
Try it yourself: Create a bar plot of the
genderfeature using ggplot2. Experiment with adding colour fills or percentage labels. This short exercise reinforces the basic structure of bar plots before we examine categorical relationships in more detail.
Class imbalance is more than a descriptive observation. When a dataset contains substantially more observations in one class than another, some algorithms tend to favour the majority class, which can lead to biased predictions and reduced sensitivity to the minority outcome. We return to this issue in Chapter 6, Section 6.5.
Having established the overall distribution of the target feature, we now examine how the remaining categorical features relate to churn. These comparisons help identify customer segments and behavioural patterns that may indicate elevated attrition risk.
Relationship Between Gender and Churn
Among the demographic features, gender provides a straightforward starting point for examining whether retention behaviour differs between male and female account holders. Although gender is not typically a strong predictor of churn in financial services, even small differences can offer insight into customer engagement patterns.
ggplot(data = churnCredit) +
geom_bar(aes(x = gender, fill = churn))
ggplot(data = churnCredit) +
geom_bar(aes(x = gender, fill = churn), position = "fill") 
The left panel displays the number of churners and non-churners within each gender group. The right panel shows proportions, which makes relative differences easier to compare. Both plots indicate that the churn rate is slightly higher among female customers. The difference, however, is small and unlikely to be practically meaningful on its own.
To examine this pattern more closely, we can inspect the contingency table:
addmargins(table(churnCredit$churn, churnCredit$gender,
dnn = c("Churn", "Gender")))
Gender
Churn female male Sum
yes 930 697 1627
no 4428 4072 8500
Sum 5358 4769 10127The table confirms the visual impression: the proportion of female customers who churn is marginally higher than that of male customers. This small difference may reflect minor behavioural or engagement variations rather than any systematic or policy-related factor.
From an analytical perspective, this suggests that gender is not a major differentiating feature for churn behaviour. More substantial variation is typically explained by behavioural and financial indicators such as transaction activity, credit utilisation, and the number of customer service contacts, which provide stronger predictive value in most churn modelling contexts.
Try it yourself: Compute the churn rate separately for male and female customers using the churnCredit dataset. Then create your own bar plot and compare it with the figures above. Based on the observed proportions, would you expect the difference in churn rates to be statistically significant? We return to this question formally in the next chapter (Section 5.8), where the test for two proportions is introduced.
Relationship Between Card Category and Churn
Card type is one of the most informative service features in the churnCredit dataset. The variable card.category places customers into four tiers: blue, silver, gold, and platinum. These categories reflect different benefit levels and often correspond to distinct customer segments.
ggplot(data = churnCredit) +
geom_bar(aes(x = card.category, fill = churn)) +
labs(x = "Card Category", y = "Count")
ggplot(data = churnCredit) +
geom_bar(aes(x = card.category, fill = churn), position = "fill") +
labs(x = "Card Category", y = "Proportion")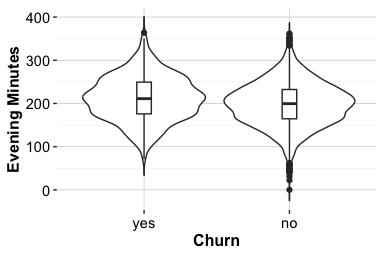
The left panel displays the number of churners and non-churners within each card tier. The right panel shows proportions within each tier. The distribution is highly imbalanced: more than 93 percent of customers hold a blue card, the entry-level option. This reflects typical product portfolios in retail banking, where most customers hold standard cards. Because the other categories are much smaller, differences across tiers must be interpreted with care.
addmargins(table(churnCredit$churn, churnCredit$card.category,
dnn = c("Churn", "Card Category")))
Card Category
Churn blue silver gold platinum Sum
yes 1519 82 21 5 1627
no 7917 473 95 15 8500
Sum 9436 555 116 20 10127The contingency table confirms the visual pattern. Churn rates are slightly higher among blue and silver cardholders and lower among customers with gold or platinum cards. Although modest, this difference suggests that customers with premium cards are more engaged and therefore less likely to close their accounts.
Because the silver, gold, and platinum groups are relatively small, analysts often combine similar categories to ensure adequate group sizes for modelling. A common approach is to separate “blue” from “silver+” (a combined group of silver, gold, and platinum cardholders). This simplification reduces sparsity, stabilises estimates, and often produces clearer and more interpretable models.
Try it yourself: Reclassify the card categories into two groups, “blue” and “silver+”, using the
fct_collapse()function from the forcats package (as in Section 3.10). Then recreate both bar plots and compare the patterns. Does the simplified version make the churn differences easier to see? Would this reclassification improve interpretability in a predictive model?
Relationship Between Income and Churn
Income level reflects purchasing power and financial stability, both of which may influence a customer’s likelihood of closing a credit account. The feature income in the churnCredit dataset includes five ordered categories, ranging from less than $40K to over $120K. Because missing values were imputed earlier, the feature now provides a complete and consistent basis for comparison.
ggplot(data = churnCredit) +
geom_bar(aes(x = income, fill = churn)) +
labs(x = "Annual Income Bracket", y = "Count") +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
ggplot(data = churnCredit) +
geom_bar(aes(x = income, fill = churn), position = "fill") +
labs(x = "Annual Income Bracket", y = "Proportion") +
theme(axis.text.x = element_text(angle = 45, hjust = 1))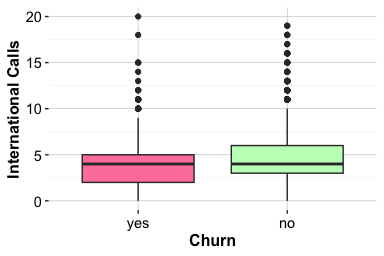
The bar plots indicate a gradual decline in churn as income increases. Customers in the lowest bracket (less than $40K) churn slightly more often than those in higher brackets, while customers earning over $120K show the lowest churn rates. Although the trend is modest, it suggests that higher-income customers maintain more stable account relationships.
addmargins(table(churnCredit$churn, churnCredit$income,
dnn = c("Churn", "Income")))
Income
Churn <40K 40K-60K 60K-80K 80K-120K >120K Sum
yes 677 310 227 271 142 1627
no 3327 1705 1345 1453 670 8500
Sum 4004 2015 1572 1724 812 10127The contingency table supports this observation. Lower-income customers may be more sensitive to service fees or constrained credit limits, while higher-income customers typically exhibit more consistent spending patterns and longer account tenure.
From an analytical perspective, income provides a weak yet interpretable signal of churn behaviour. Because the categories follow a natural progression, treating income as an ordered factor may be useful during modelling.
Try it yourself: Convert
incomeinto an ordered factor usingfactor(..., ordered = TRUE)and recreate the proportional bar plot. Does the plot change? Next, reorder the categories usingfct_relevel()and observe how the ordering affects readability. Small adjustments to factor ordering often make EDA plots easier to interpret.
Relationship Between Marital Status and Churn
Marital status may influence financial behaviour and account management, making it a useful demographic feature to explore in the context of churn. The marital feature in the churnCredit dataset includes three categories—married, single, and divorced—which may reflect differences in household structure, shared responsibilities, or spending patterns.
ggplot(data = churnCredit) +
geom_bar(aes(x = marital, fill = churn)) +
labs(x = "Marital Status", y = "Count")
ggplot(data = churnCredit) +
geom_bar(aes(x = marital, fill = churn), position = "fill") +
labs(x = "Marital Status", y = "Proportion")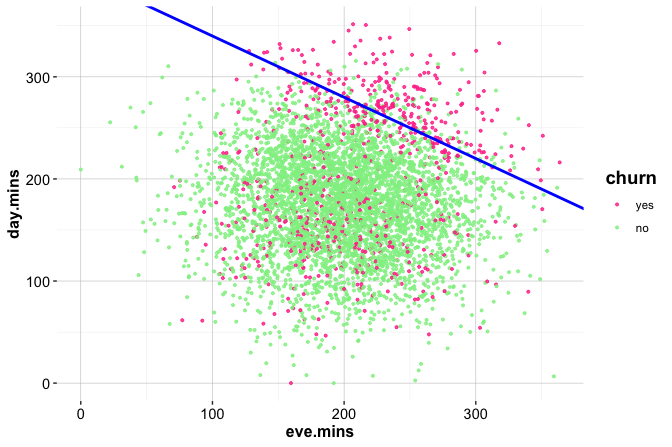
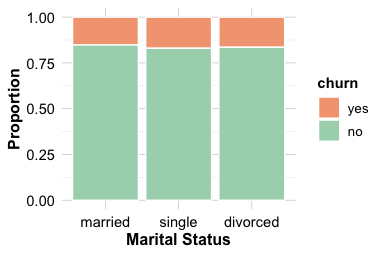
The count plot on the left shows that most customers are married, followed by single and divorced individuals. The proportional bar plot on the right highlights that single customers churn at a slightly higher rate than married or divorced customers. This difference is consistent but small, suggesting only a weak relationship between marital status and account closure.
addmargins(table(churnCredit$churn, churnCredit$marital,
dnn = c("Churn", "Marital Status")))
Marital Status
Churn married single divorced Sum
yes 767 727 133 1627
no 4277 3548 675 8500
Sum 5044 4275 808 10127The contingency table supports the visual impression. Although single customers exhibit marginally higher churn rates, the overall association between marital status and churn appears limited. Small behavioural differences may exist across household types, but marital status is unlikely to be a strong predictor of churn on its own.
From an analytical standpoint, this feature offers only minor explanatory value. Later sections will show that behavioural and financial indicators—including spending activity, utilisation ratio, and customer-service interactions—provide more substantial insight into churn risk. Because both marital and churn are categorical variables, the Chi-square test introduced in Chapter 5.9 will formally assess whether the observed differences are statistically meaningful.
Try it yourself: Examine whether
educationis associated with churn. Create bar plots for counts and proportions, inspect the contingency table, and consider whether any observed differences appear meaningful in practice. This exercise reinforces the workflow used for exploring categorical features.
4.5 Exploring Numerical Features
The churnCredit dataset contains fourteen numerical features that describe customer behaviour, credit management, and engagement with the bank. Examining these features helps identify how customers differ in spending, activity level, financial capacity, and behavioural change, factors commonly associated with churn risk. To keep the analysis focused and interpretable, this section concentrates on five representative features that capture key behavioural and financial dimensions of customer retention:
-
contacts.count.12: number of customer service contacts in the past 12 months, reflecting engagement or potential dissatisfaction; -
transaction.amount.12: total amount spent in the past 12 months, indicating overall activity on the card; -
credit.limit: assigned credit line, offering insight into financial capacity; -
months.on.book: length of the customer relationship with the bank; -
ratio.amount.Q4.Q1: ratio of spending in the fourth quarter to that in the first quarter, capturing changes in spending behaviour over time.
Together, these features offer a concise yet comprehensive view of customer interaction, engagement, financial strength, tenure, and behavioural trends. They serve as a foundation for the numerical analyses that follow, where visualisations and summary statistics are used to uncover patterns linked to churn.
Customer Contacts and Churn
The number of customer service contacts in the past year (contacts.count.12) offers insight into customer engagement and potential dissatisfaction. This feature is a count variable with small integer values, making bar plots more appropriate than boxplots or density plots. Bar plots clearly display how frequently customers interacted with support and allow easy comparison between churned and active accounts.
ggplot(data = churnCredit) +
geom_bar(aes(x = contacts.count.12, fill = churn)) +
labs(x = "Number of Contacts in Past 12 Months", y = "Count")
ggplot(data = churnCredit) +
geom_bar(aes(x = contacts.count.12, fill = churn), position = "fill") +
labs(x = "Number of Contacts in Past 12 Months", y = "Proportion")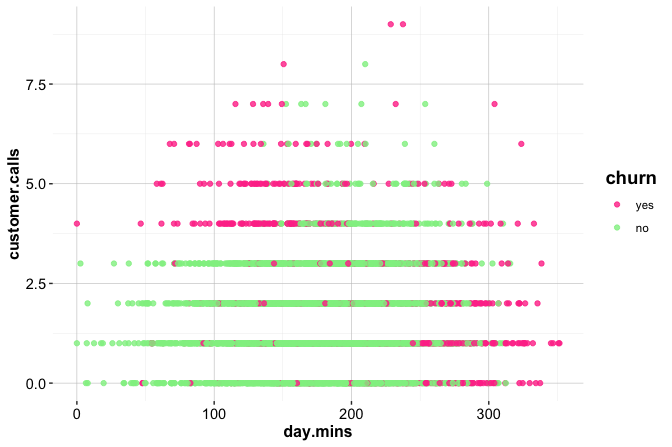
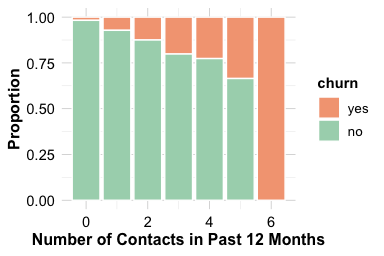
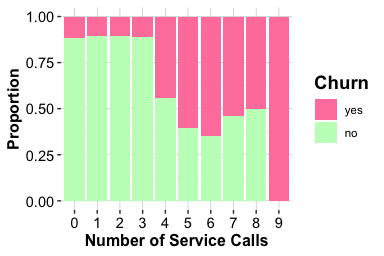
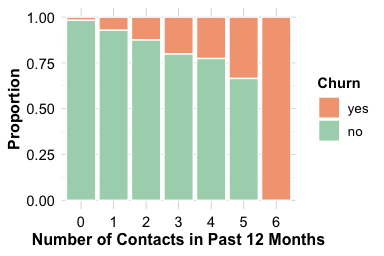
Both plots show that customers who contact customer service more frequently are more likely to churn. The increase is particularly noticeable for those with four or more interactions during the year. This pattern suggests that repeated service contacts may reflect concerns, dissatisfaction, or unresolved issues. From an analytical perspective, contacts.count.12 provides a clear behavioural signal: frequent contact is associated with elevated churn risk. Because it is easy to interpret and directly linked to customer experience, this feature often plays a meaningful role in churn modelling and early-warning retention strategies.
Transaction Amount and Churn
The total transaction amount in the past twelve months (transaction.amount.12) reflects how actively customers use their credit card. Higher spending generally indicates regular engagement and satisfaction, whereas lower spending may signal reduced interest or a shift toward alternative payment methods. Because this feature is continuous, boxplots and density plots are appropriate choices for visualizing its distribution across churn groups.
ggplot(data = churnCredit) +
geom_boxplot(aes(x = churn, y = transaction.amount.12),
fill = c("#F4A582", "#A8D5BA")) +
labs(x = "Churn", y = "Total Transaction Amount (12 months)")
ggplot(data = churnCredit) +
geom_density(aes(x = transaction.amount.12, fill = churn), alpha = 0.6) +
labs(x = "Total Transaction Amount (12 months)", y = "Density")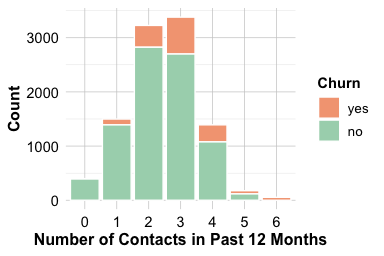
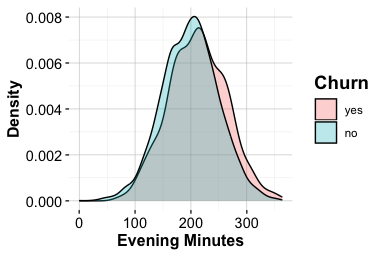
Both plots reveal a clear difference between churners and non-churners. Customers who churn tend to have lower total transaction amounts and a narrower spread of spending, suggesting limited engagement throughout the year. In contrast, active customers exhibit higher and more varied transaction volumes.
From a business perspective, sustained reductions in spending can serve as an early indicator of disengagement. Monitoring spending trends and offering timely interventions—such as usage-based rewards or personalised incentives—may help retain customers who show declining activity.
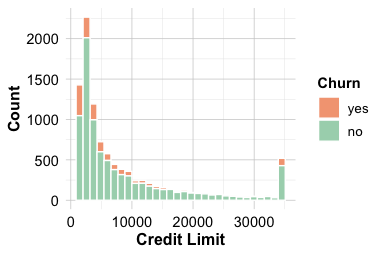
Credit Limit and Churn
The total credit line assigned to a customer (credit.limit) reflects financial capacity and the bank’s assessment of creditworthiness. Customers with higher credit limits are often more established or historically reliable, which may also make them less likely to close their accounts. Because credit limits vary widely across customers, violin plots and histograms provide useful perspectives on both the distribution shape and the level differences between churn groups.
ggplot(data = churnCredit, aes(x = churn, y = credit.limit, fill = churn)) +
geom_violin(trim = FALSE) +
labs(x = "Churn", y = "Credit Limit")
ggplot(data = churnCredit) +
geom_histogram(aes(x = credit.limit, fill = churn)) +
labs(x = "Credit Limit", y = "Count")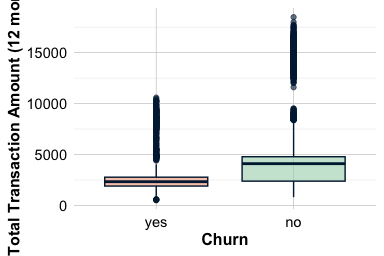
Both plots indicate that customers who churn tend to have noticeably lower credit limits. The distribution for active customers is broader and shifted toward higher values, suggesting that individuals with greater available credit are more engaged and less inclined to close their accounts.
From a business perspective, this pattern highlights a segment that may benefit from targeted retention strategies. Customers with relatively small credit limits might feel constrained or see limited value in maintaining their accounts. Offering appropriate credit line increases to eligible customers or tailoring card benefits to lower-limit users could help strengthen engagement and reduce churn risk.
Months on Book and Churn
The feature months.on.book measures how long a customer has held their credit card account. Tenure often reflects relationship stability, accumulated benefits, and familiarity with the service. Customers with longer histories typically show stronger loyalty, whereas newer customers may be more vulnerable to unmet expectations or early dissatisfaction.
ggplot(data = churnCredit, aes(x = churn, y = months.on.book, fill = churn)) +
geom_violin(alpha = 0.5, trim = TRUE) +
geom_boxplot(width = 0.15, fill = "white", outlier.shape = NA) +
labs(x = "Churn", y = "Months on Book") +
theme(legend.position = "none")
ggplot(data = churnCredit) +
geom_histogram(aes(x = months.on.book, fill = churn), bins = 20) +
labs(x = "Months on Book", y = "Count")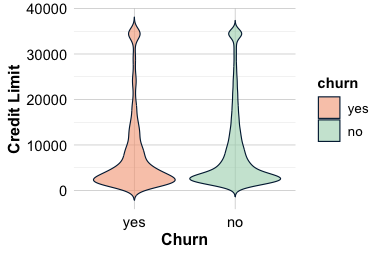
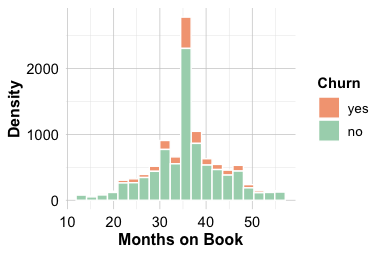
Both plots suggest that customers who churn tend to have slightly shorter tenures than those who remain active. The difference is not large, but it is consistent: the median tenure for churners is lower by a few months. The pronounced peak around 36 months likely reflects a cohort effect, possibly linked to a major acquisition campaign that occurred three years prior to the observation period.
From a business perspective, these patterns highlight the importance of early relationship management. Targeted onboarding, proactive engagement in the first year, and timely communication may help build loyalty among newer customers and reduce attrition during the initial stages of the customer lifecycle.
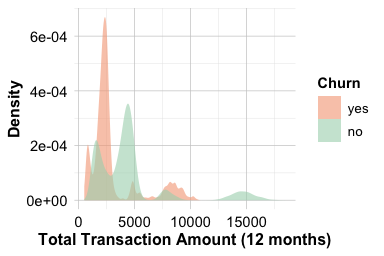
Ratio of Transaction Amount (Q4/Q1) and Churn
The feature ratio.amount.Q4.Q1 compares total spending in the fourth quarter with that in the first quarter. It captures how customer behaviour changes over time and provides a temporal view of engagement. A ratio below 1 indicates that spending in Q4 was lower than in Q1, whereas a ratio above 1 reflects increased spending toward the end of the year.
ggplot(data = churnCredit) +
geom_boxplot(aes(x = churn, y = ratio.amount.Q4.Q1),
fill = c("#F4A582", "#A8D5BA")) +
labs(x = "Churn", y = "Transaction Amount Ratio (Q4/Q1)")
ggplot(data = churnCredit) +
geom_density(aes(x = ratio.amount.Q4.Q1, fill = churn), alpha = 0.6) +
labs(x = "Transaction Amount Ratio (Q4/Q1)", y = "Density")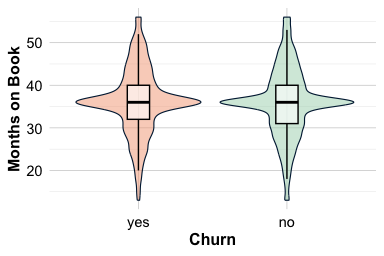
The plots show that customers who churn tend to have lower Q4-to-Q1 ratios, indicating a reduction in spending toward the end of the year. Customers who remain active typically maintain or modestly increase their spending. This downward shift in activity may serve as an early sign of disengagement: gradual reductions in spending often precede account closure.
From a business perspective, monitoring quarterly spending patterns can help identify customers who may be at risk of churn. Seasonal incentives or targeted engagement campaigns aimed at customers with declining activity may help maintain their involvement and improve retention outcomes.
Try it yourself: Repeat the analysis using features such as
ageandmonths.inactive. Compare the patterns you observe for churners and non-churners. How might these features contribute to predicting which customers are likely to remain active?
4.6 Exploring Multivariate Relationships
Univariate and pairwise analyses provide helpful context, but real-world customer behaviour often arises from the interaction of multiple features. Examining these joint patterns is essential for identifying customer segments with distinct churn risks and for selecting features that add genuine value to predictive models.
We begin with a correlation analysis of the numerical features, which highlights pairs of variables that move together and helps detect redundancy. After establishing these relationships, we broaden the analysis to explore how behavioural, transactional, and demographic features interact. These multivariate views reveal usage patterns and customer profiles that are not visible through individual variables alone.
4.6.1 Assessing Correlation and Redundancy
Before analyzing more complex interactions among features, it is helpful to assess how numerical features relate to one another. Correlation analysis helps identify features that may carry overlapping information or exhibit redundancy. Recognizing such relationships early simplifies the modeling process and reduces the risk of multicollinearity.
Correlation quantifies how two features move together. A positive correlation means that as one feature increases, the other tends to increase as well; a negative correlation suggests that one decreases as the other increases. The Pearson correlation coefficient, denoted by \(r\), summarizes this relationship on a scale from \(-1\) to \(1\). A value of \(r = 1\) indicates a perfect positive relationship, \(r = -1\) a perfect negative relationship, and \(r = 0\) no linear association.
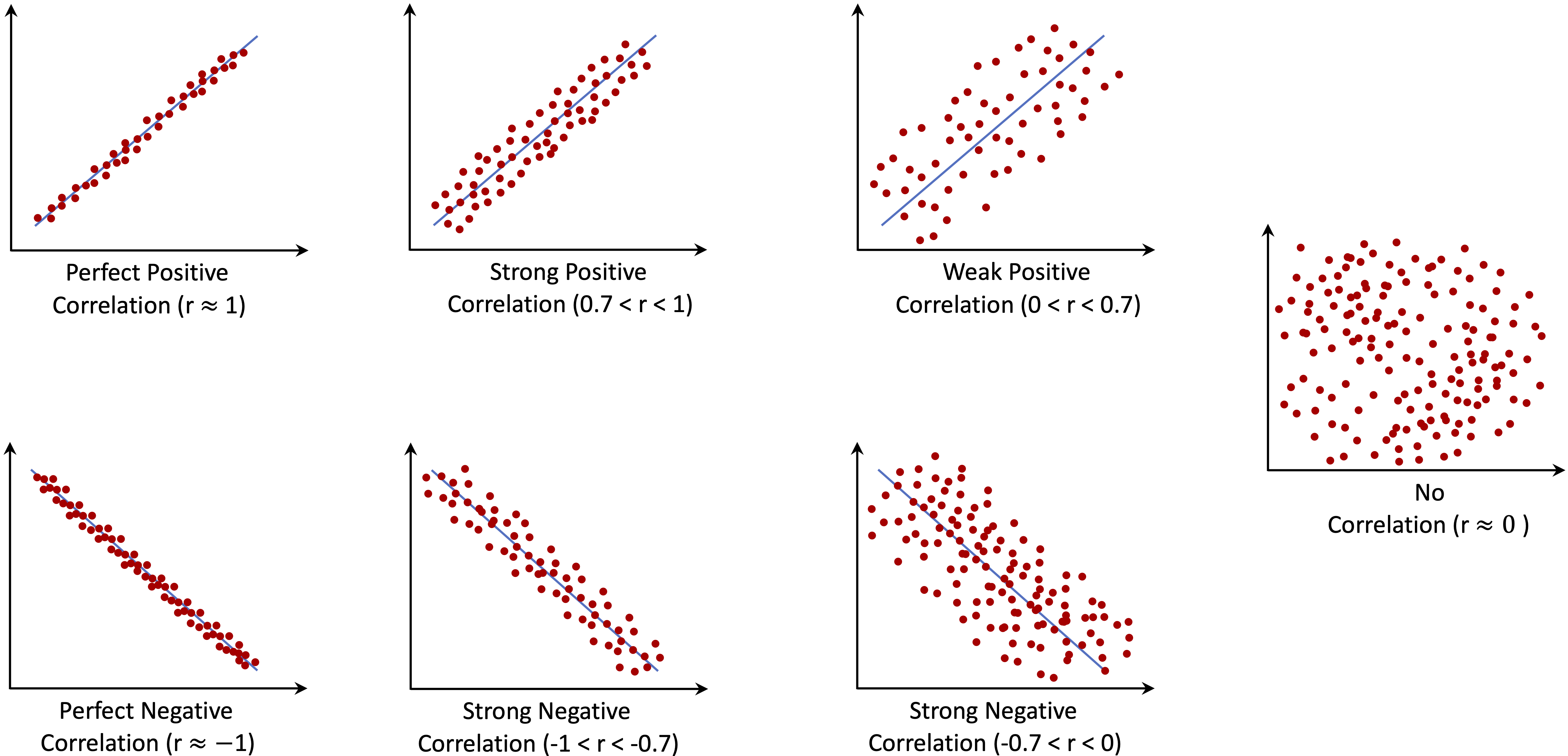
Note: Correlation does not imply causation. For example, a strong positive correlation between customer contacts and churn does not mean that contacting customer service causes customers to leave. Both behaviours may stem from an underlying factor, such as dissatisfaction with service.
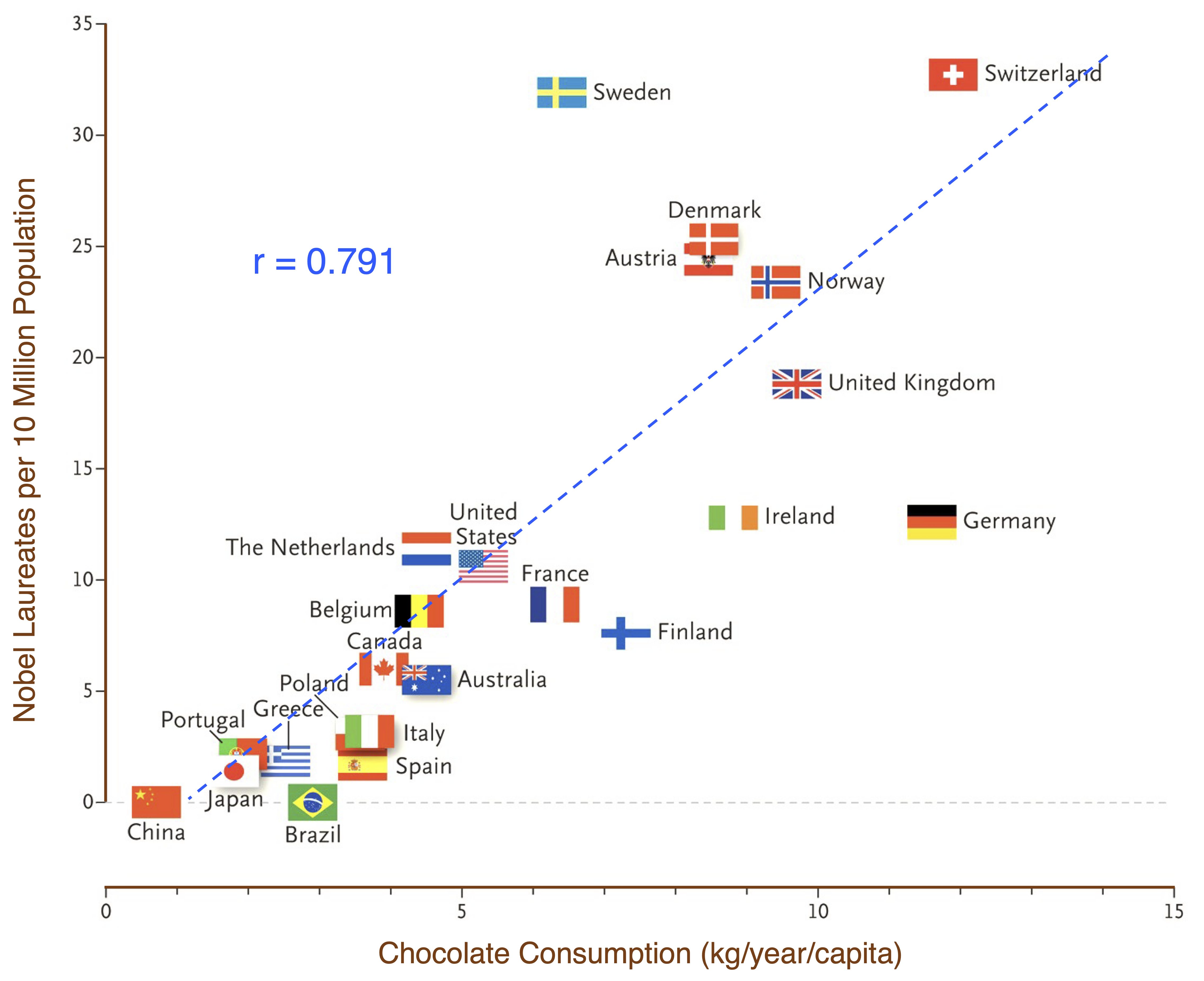
To illustrate this point, Figure 4.3 shows a well-known example from Messerli (2012), depicting a strong correlation between per-capita chocolate consumption and Nobel Prize wins across countries. Although amusing, it underscores the importance of caution: correlations may arise by coincidence or through the influence of unobserved factors. For readers interested in causality, The Book of Why by Judea Pearl and Dana Mackenzie (pearl2018book?) offers an accessible introduction to this topic.
Returning to the churnCredit dataset, we compute and visualize the correlation matrix for all numerical features using a heatmap. This visualization helps detect redundant or related features before modeling.
library(ggcorrplot)
numeric_features = c("age", "dependent.count", "months.on.book",
"relationship.count", "months.inactive", "contacts.count.12",
"credit.limit", "revolving.balance", "available.credit",
"transaction.amount.12", "transaction.count.12",
"ratio.amount.Q4.Q1", "ratio.count.Q4.Q1", "utilization.ratio")
cor_matrix = cor(churnCredit[, numeric_features])
ggcorrplot(cor_matrix, type = "lower", lab = TRUE, lab_size = 2, tl.cex = 6,
colors = c("#699fb3", "white", "#b3697a"),
title = "Visualization of the Correlation Matrix")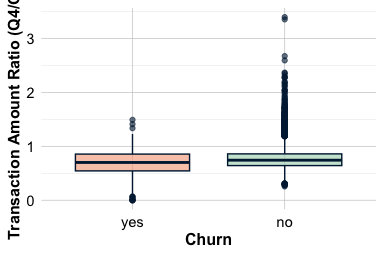
The heatmap shows that most numerical features in the churnCredit dataset are only moderately or weakly correlated, suggesting that they capture distinct behavioural dimensions. One notable exception is the perfect correlation (\(r = 1\)) between credit.limit and available.credit, indicating that one is mathematically derived from the other. Including both in a model would therefore add redundancy without contributing new information. This relationship can be seen in the following pair of scatter plots:
ggplot(data = churnCredit) +
geom_point(aes(x = credit.limit, y = available.credit), size = 0.1) +
labs(x = "Credit Limit", y = "Available Credit")
ggplot(data = churnCredit) +
geom_point(aes(x = credit.limit - revolving.balance,
y = available.credit), size = 0.1) +
labs(x = "Credit Limit - Revolving Balance", y = "Available Credit")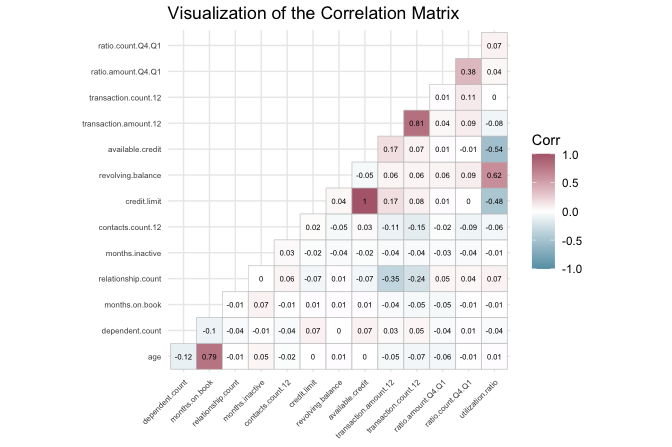
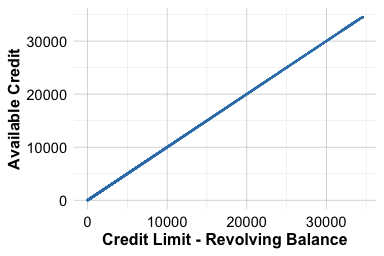
The first plot shows the perfect linear relationship between credit.limit and available.credit. The second confirms that available.credit is essentially equal to credit.limit - revolving.balance, validating the redundancy observed in the correlation matrix.
Optional exploration: Because
credit.limit,available.credit, andrevolving.balanceare mathematically linked, their joint structure can also be examined using a 3D plot. The plotly package allows interactive rotation and zooming, which can make this linear relationship especially clear. The following code works in HTML output or in your editor (such as RStudio), but it will not render in the PDF version of this book. This 3D perspective shows that all three features lie close to a plane, reflecting the identityavailable.credit = credit.limit − revolving.balance.
library(plotly)
plot_ly(
data = churnCredit,
x = ~credit.limit,
y = ~available.credit,
z = ~revolving.balance,
color = ~churn,
colors = c("#F4A582", "#A8D5BA"),
type = "scatter3d",
mode = "markers",
marker = list(size = 1)
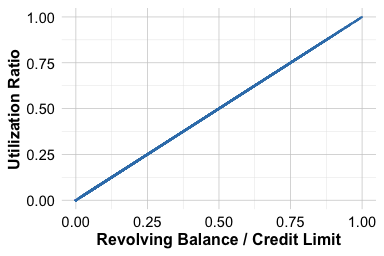
)A similar relationship is observed between utilization.ratio, revolving.balance, and credit.limit. The utilization ratio is mathematically defined as revolving.balance / credit.limit, meaning it does not introduce new information but provides a normalized view of credit usage. Depending on the modeling goal, it may be preferable to retain either the ratio for interpretability or its component features for more detailed financial analysis.
ggplot(data = churnCredit) +
geom_point(aes(x = credit.limit, y = utilization.ratio), size = 0.1) +
labs(x = "Credit Limit", y = "Utilization Ratio")
ggplot(data = churnCredit) +
geom_point(aes(x = revolving.balance/credit.limit,
y = utilization.ratio), size = 0.1) +
labs(x = "Revolving Balance / Credit Limit", y = "Utilization Ratio")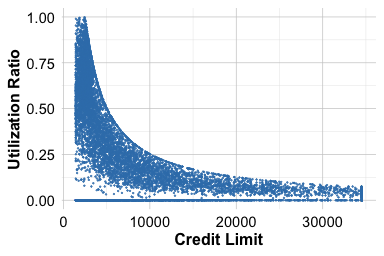
Try it yourself: Create a 3D scatter plot using the features
credit.limit,revolving.balance, andutilization.ratio. These three measures are mathematically linked, so the points should lie close to a plane. Use plotly to explore the structure interactively. Rotate the plot and examine how the features relate. Does the 3D view make the redundancy among these features more visually apparent?
Identifying redundant or highly correlated features provides a clearer foundation for multivariate exploration. Once derived features are removed or consolidated, the remaining numerical features offer complementary perspectives on customer behaviour. The next subsection examines how key features interact with one another, beginning with joint patterns in spending amount and transaction frequency. These multivariate visualisations reveal usage dynamics that are not apparent from individual features alone and help identify customer segments with distinct churn tendencies.
Joint Patterns in Transaction Amount and Count
Transaction activity has two important dimensions: how much customers spend and how often they use their card. The features transaction.amount.12 and transaction.count.12 capture these behaviours over a twelve-month period. Examining them together provides insight into usage patterns that are not visible through univariate plots. A scatter plot with marginal histograms is particularly helpful because it shows both the joint structure and the separate distributions of each feature.
The code below first constructs a base scatter plot using ggplot2 and then applies ggMarginal() from the ggExtra package to add histograms along the horizontal and vertical axes:
library(ggExtra)
# Base scatter plot
scatter_plot <- ggplot(data = churnCredit) +
geom_point(aes(x = transaction.amount.12, y = transaction.count.12,
color = churn), size = 0.1, alpha = 0.7) +
labs(x = "Transaction Amount", y = "Total Transaction Count (12 months)") +
theme(legend.position = "bottom")
# Add marginal histograms
ggMarginal(scatter_plot, type = "histogram", groupColour = TRUE,
groupFill = TRUE, alpha = 0.6, size = 4)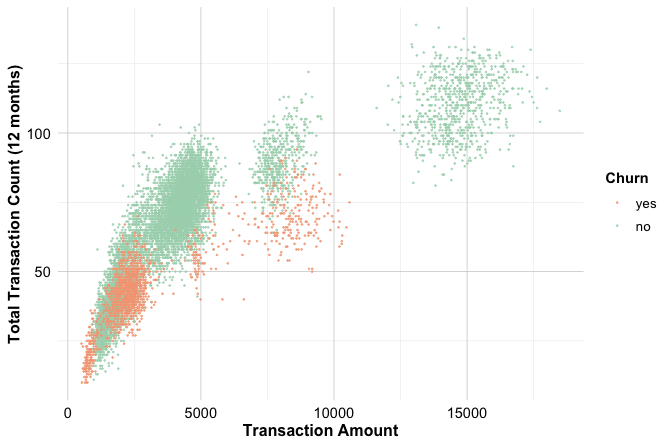
The central scatter plot reveals a clear positive association: customers who spend more also tend to make more transactions. Most observations form a broad diagonal band of moderate spending and activity, where churners and non-churners largely overlap. The marginal histograms provide a quick comparison of the individual distributions for both features, making differences between churn groups easier to notice.
Try it yourself: Replace
type = "histogram"withtype = "density"inggMarginal()to add marginal density curves. Then recreate the scatter plot usingratio.amount.Q4.Q1on the horizontal axis instead oftransaction.amount.12. Which combination makes churn differences easier to see?
To highlight specific usage patterns, we focus on two illustrative segments: customers with very low spending and customers with moderate spending but relatively few transactions. These subsets are extracted using the subset() function as follows:
sub_churnCredit = subset(
churnCredit,
(transaction.amount.12 < 1000) |
((2000 < transaction.amount.12) &
(transaction.amount.12 < 3000) &
(transaction.count.12 < 52))
)
ggplot(data = sub_churnCredit,
aes(x = churn,
label = scales::percent(prop.table(after_stat(count))))) +
geom_bar(fill = c("#F4A582", "#A8D5BA")) +
geom_text(stat = "count", vjust = 0.4, size = 8) 
Within this subset, the proportion of churners is noticeably higher than in the full dataset. These patterns suggest that customers with low or inconsistent usage—particularly those who spend little and use their card infrequently—face a higher risk of churn.
From a modelling perspective, this example illustrates the value of examining feature interactions: neither transaction amount nor count alone identifies these customers, but their combination does. From a business perspective, these low-activity customers represent an opportunity for targeted re-engagement through personalised communication or usage-based incentives.
Card Category and Spending Patterns
The feature card.category divides customers into four product tiers (blue, silver, gold, and platinum). The feature transaction.amount.12 measures the total amount spent over the past twelve months. Examining these features together provides insight into how card tier relates to spending behaviour. Because transaction.amount.12 is continuous and card.category is categorical, density plots are a natural choice for comparing entire distributions. They highlight differences in the shape, centre, and spread of spending among card tiers.
ggplot(data = churnCredit, aes(x = transaction.amount.12, fill = card.category)) +
geom_density(alpha = 0.5) +
labs(x = "Total Transaction Amount (12 months)",
y = "Density",
fill = "Card Category") +
scale_fill_manual(values = c("#1E90FF", "#C0C0C0", "#FFD700", "#E5E4E2"))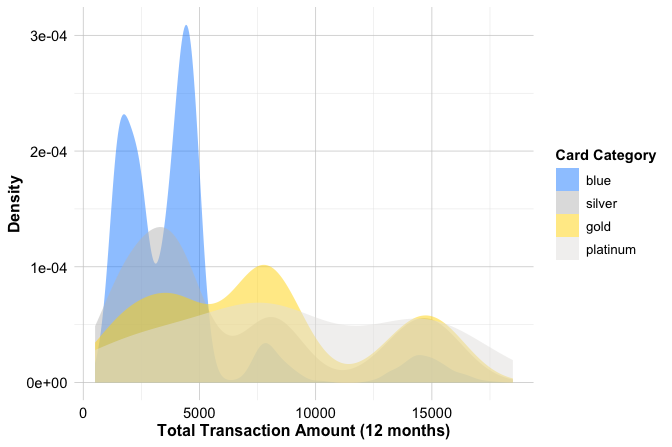
The density curves show a clear gradient across tiers: customers with gold and platinum cards tend to have noticeably higher transaction amounts. Their curves are shifted to the right relative to those of blue and silver cardholders. Blue card customers, who constitute more than 90 percent of the entire customer base, display a broader distribution concentrated in the lower and middle spending ranges. Although this imbalance affects how prominent each curve appears, the underlying pattern remains consistent: higher-tier cards are associated with greater spending activity.
From a business perspective, this relationship is intuitive. Premium cardholders typically receive enhanced benefits, rewards, or services, and they often belong to customer segments with higher financial engagement. Blue cardholders, by contrast, form a mixed group ranging from highly active customers to those who use their card only occasionally. These observations can guide differentiated retention and marketing strategies—for example, offering targeted upgrades to high-spending blue cardholders or designing tailored benefits to encourage greater engagement among lower-activity segments.
Transaction Analysis by Age
Age is an important demographic factor that can shape financial behaviour, spending patterns, and overall engagement with credit products. In the churnCredit dataset, examining how transaction activity varies across age helps determine whether younger and older customers display different usage profiles that might influence their likelihood of churn. Because individual observations form a dense cloud, we use smoothed trend lines to highlight the overall relationship between age and transaction activity.
# Total Transaction Amount by Age
ggplot(data = churnCredit,
aes(x = age, y = transaction.amount.12, color = churn)) +
geom_smooth(se = FALSE, linewidth = 1.1, alpha = 0.9) +
labs(x = "Customer Age", y = "Total Transaction Amount (12 months)")
# Total Transaction Count by Age
ggplot(data = churnCredit,
aes(x = age, y = transaction.count.12, color = churn)) +
geom_smooth(se = FALSE, linewidth = 1.1, alpha = 0.9) +
labs(x = "Customer Age", y = "Total Transaction Count (12 months)") 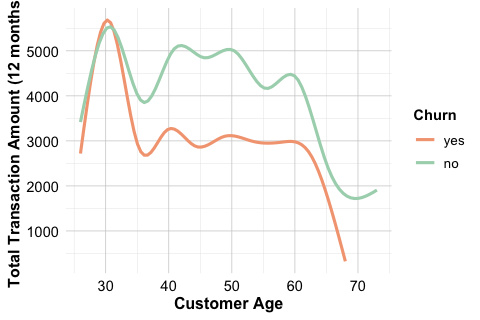

The smooth curves indicate that both spending and transaction frequency tend to decline with age. Younger customers generally make more purchases and spend larger amounts, whereas older customers show lower and more stable levels of activity. There is a slight separation between churners and non-churners at younger ages: highly active younger customers appear somewhat more likely to churn, though the difference is modest.
These patterns emphasise that age alone does not determine churn. Instead, demographic characteristics interact with behavioural indicators to shape retention dynamics. Considering age jointly with measures of spending, engagement, and credit usage provides a more complete picture of customer behaviour than any single feature on its own.
4.7 Summary of Exploratory Findings
The exploratory analysis of the churnCredit dataset provides a multifaceted view of customer behaviour and the factors associated with churn. By examining categorical features, numerical features, and their interactions, several consistent patterns emerge that are relevant for understanding and modelling customer attrition.
Demographic characteristics show only weak associations with churn. Gender and marital status exhibit small differences in churn rates, and education and income levels display modest variation once other factors are considered. These variables may provide supporting context in modelling but do not appear to be primary drivers of account closure. In contrast, service-related characteristics such as card category and income bracket offer clearer signals. Customers with higher-tier cards and those in higher income groups churn less often, suggesting that perceived value and financial capacity contribute to account stability.
The numerical features reveal stronger and more actionable patterns. Customers who contact customer service frequently, particularly four or more times within a year, churn at higher rates. This suggests that repeated service interactions may reflect dissatisfaction or unresolved problems. Spending activity, measured by total transaction amount over twelve months, shows a similarly strong relationship with retention. Active customers display higher and more varied spending, whereas churners typically have substantially lower transaction volumes. Declines in spending may therefore serve as early indicators of disengagement.
Credit-related features add further insight. Customers with lower credit limits are somewhat more likely to leave, while those with higher limits tend to remain active. This pattern may relate to differences in financial standing or to perceived benefits associated with higher credit availability. Tenure shows a modest but consistent relationship: customers with longer account histories are slightly less likely to churn, indicating that new customers may require additional support during the early stages of their relationship with the bank. The ratio of fourth-quarter to first-quarter spending highlights behavioural change over time. Churners often show declining spending in the later part of the year, whereas active customers tend to maintain or increase their usage. This dynamic measure is particularly useful for detecting emerging signs of disengagement.
Multivariate exploration deepens these insights. Joint analysis of transaction amount and transaction count shows that customers who both spend little and use their card infrequently have elevated churn rates. This relationship does not emerge as clearly from the individual features and demonstrates the importance of considering interactions. Combining card category with transaction amount reveals that higher-tier cardholders tend to spend more and churn less, while blue cardholders represent a more heterogeneous group that includes many low-activity accounts. Analysis across age groups shows that younger customers generally spend more and complete more transactions but experience slightly higher churn rates than older customers with comparable activity levels. This aligns with broader evidence that younger customers are more willing to switch providers.
The correlation analysis identifies a few redundant features. Available credit is determined by subtracting revolving balance from the credit limit, and the utilisation ratio is calculated from revolving balance and credit limit. These relationships indicate that the derived features do not contain additional information beyond their components. For modelling, it is often preferable to retain either the raw components or the ratio, depending on the analytical objective, rather than all three. Removing such redundant variables simplifies the feature set and reduces the risk of multicollinearity.
Overall, the exploratory analysis shows that churn is more closely associated with behavioural and financial indicators, such as spending activity, credit usage, and service interactions, than with demographic variables alone. Together, these findings provide a clear empirical foundation for the statistical inference and predictive modelling in the chapters that follow. Several of the patterns identified here will be examined formally in Chapter 5 using hypothesis tests to assess whether these observed differences reflect wider population-level effects.
4.8 Chapter Summary and Takeaways
This chapter showed how exploratory data analysis supports the transition from raw data to statistical modelling. Using the churnCredit dataset, we applied graphical and numerical techniques to examine the structure of the data, identify potential issues, and develop hypotheses about customer behaviour.
The analysis began with an overview of the dataset and an initial preparation step, where missing values encoded as “unknown” were identified and resolved. Ensuring that features were clean and correctly typed created a sound basis for exploration. We then examined categorical features such as gender, education, marital status, income, and card type to understand customer profiles. Numerical features such as credit limit, transaction activity, and utilisation ratio provided additional insight into financial and behavioural patterns.
The exploratory results revealed several consistent relationships. Customers with smaller credit limits, higher utilisation ratios, or frequent customer service interactions were more likely to churn. In contrast, customers with higher transaction amounts and lower utilisation tended to remain active. These observations demonstrate how EDA can highlight potential explanatory features before any formal modelling is undertaken.
Multivariate exploration further showed how combinations of features interact to shape churn behaviour. Joint patterns in transaction amount and transaction count, connections between card category and spending, and links between age and financial activity illustrated that churn often arises from a combination of behavioural, financial, and demographic factors rather than isolated characteristics.
The chapter also emphasised the importance of identifying redundant features. For example, available credit and utilisation ratio were found to be deterministically related to other features in the dataset. Recognising such redundancy simplifies later modelling and improves interpretability.
Taken together, the examples in this chapter highlight three guiding principles for effective exploratory analysis. First, graphical and numerical summaries work best when used together to provide complementary insights. Second, careful attention to data quality, including missing values and redundant features, is essential for reliable analysis. Third, EDA is not only descriptive: it offers direction for statistical inference and predictive modelling by revealing patterns worth investigating further.
The results of this chapter form the empirical foundation for the next stage of the analysis. Chapter 5 introduces the tools of statistical inference, which allow us to formalise uncertainty, quantify relationships, and test hypotheses suggested by the exploratory findings.
4.9 Exercises
This section provides exercises designed to consolidate the concepts and techniques introduced in this chapter. The questions cover conceptual understanding, hands-on data exploration, and integrative challenges. Exercises begin with short interpretive questions, followed by applied analysis using the churn and bank datasets, and conclude with advanced problems that encourage synthesis and critical reflection.
Conceptual Questions
Why is exploratory data analysis essential before building predictive models? What risks might arise if this step is skipped?
If a feature does not show a clear relationship with the target during EDA, should it be excluded from modeling? Consider potential interactions, hidden effects, and the role of feature selection.
What does it mean for two features to be correlated? Explain the direction and strength of correlation, and contrast correlation with causation using an example.
How can correlated predictors be detected and addressed during EDA? Describe how this improves model performance and interpretability.
What are the potential consequences of including highly correlated features in a predictive model? Discuss the effects on accuracy, interpretability, and model stability.
Is it always advisable to remove one of two correlated predictors? Under what circumstances might keeping both be justified?
For each of the following methods—histograms, box plots, density plots, scatter plots, summary statistics, correlation matrices, contingency tables, and bar plots—indicate whether it applies to categorical data, numerical data, or both. Briefly describe its role in EDA.
A bank observes that customers with high credit utilization and frequent customer service interactions are more likely to close their accounts. What actions could the bank take in response, and how might this guide retention strategy?
Suppose several pairs of features in a dataset have high correlation (for example, \(r > 0.9\)). How would you handle this to ensure robust and interpretable modeling?
Why is it important to consider both statistical and practical relevance when evaluating correlations? Provide an example of a statistically strong but practically weak correlation.
Why is it important to investigate multivariate relationships in EDA? Describe a case where an interaction between two features reveals a pattern that univariate analysis would miss.
How does data visualization support EDA? Provide two specific examples where visual tools reveal insights that summary statistics might obscure.
Suppose you discover that customers with both high credit utilization and frequent service calls are more likely to churn. What business strategies might be informed by this finding?
What are some common causes of outliers in data? How would you decide whether to retain, modify, or exclude an outlier?
Why is it important to address missing values during EDA? Discuss strategies for handling missing data and when each might be appropriate.
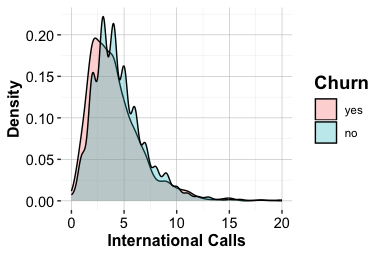
Hands-On Practice: Exploring the churn Dataset
The churn dataset from the R package liver contains information about customer behavior and service usage in a telecommunications company. The objective is to identify patterns associated with customer churn—whether a customer has left the service. This dataset was also explored earlier in this chapter and will be revisited in later chapters for classification modeling. This dataset will be used for classification in the case study of Chapter 10. More details are available at https://rdrr.io/cran/liver/man/churn.html.
To load and inspect the dataset:
Summarize the structure of the dataset and identify feature types. What information does this provide about the nature of the data?
Examine the target feature
churn. What proportion of customers have left the service?Explore the relationship between
intl.planandchurn. Use bar plots and contingency tables to describe what you find.Analyze the distribution of
customer.calls. Which values occur most frequently? What might this indicate about customer engagement or dissatisfaction?Investigate whether customers with higher
day.minsare more likely to churn. Use box plots or density plots to support your reasoning.Compute the correlation matrix for all numerical features. Which features show strong relationships, and which appear independent?
Summarize your main EDA findings. What patterns emerge that could be relevant for predicting churn?
Reflect on business implications. Which customer behaviors appear most strongly associated with churn, and how could these insights inform a retention strategy?
Hands-On Practice: Exploring the bank Dataset
The bank dataset from the R package liver contains data on direct marketing campaigns of a Portuguese bank. The objective is to predict whether a client subscribes to a term deposit. This dataset will be used for classification in the case study of Chapter 12. More details are available at https://rdrr.io/cran/liver/man/bank.html.
To load and inspect the dataset:
Summarize the structure and feature types. What does this reveal about the dataset?
Plot the target feature
deposit. What proportion of clients subscribed to a term deposit?Explore the features
default,housing, andloanusing bar plots and contingency tables. What patterns emerge?Visualize the distributions of numerical features using histograms and box plots. Note any skewness or unusual observations.
Identify outliers among numerical features. What strategies would you consider for handling them?
Compute and visualize correlations among numerical features. Which features are highly correlated, and how might this influence modeling decisions?
Summarize your main EDA observations. How would you present these results in a report?
Interpret your findings in business terms. What actionable conclusions could the bank draw from these patterns?
Examine whether higher values of
campaign(number of contacts) relate to greater subscription rates. Visualize and interpret.Propose one new feature that could improve model performance based on your EDA findings.
Investigate subscription rates by
month. Are some months more successful than others?Explore how
jobrelates todeposit. Which occupational groups have higher success rates?Analyze the joint impact of
educationandjobon subscription outcomes. What patterns do you observe?Examine whether the
durationof the last contact influences the likelihood of a positive outcome.Compare success rates across campaigns. What strategies might these differences suggest?
Challenge Problems
Create a concise one- or two-plot summary of an EDA finding from the bank dataset. Focus on clarity and accessibility for a non-technical audience, using brief annotations to explain the insight.
Using the adult dataset, identify a subgroup likely to earn over $50K. Describe their characteristics and how you uncovered them through EDA.
A feature appears weakly related to the target in univariate plots. Under what conditions could it still improve model accuracy?
Examine whether the proportion of
depositoutcomes differs bymaritalstatus orjobcategory. What hypotheses could you draw from these differences?Using the adult dataset, identify predictors that may not contribute meaningfully to modeling. Justify your selections with evidence from EDA.
Self-Reflection
Reflect on what you have learned in this chapter. Consider the following questions as a guide:
- How has exploratory data analysis changed your understanding of the dataset before modeling?
- Which visualizations or summary techniques did you find most effective for revealing structure or patterns?
- When exploring data, how do you balance curiosity-driven discovery with methodological discipline?
- How can EDA findings influence later stages of the data science workflow, such as feature engineering, model selection, or evaluation?
- In what ways did EDA help you detect issues of data quality, such as missing values or redundancy?
EDA is not a one-time step but an iterative mindset that continues throughout analysis. Revisiting exploratory findings after modeling often deepens understanding and improves both model performance and interpretability.